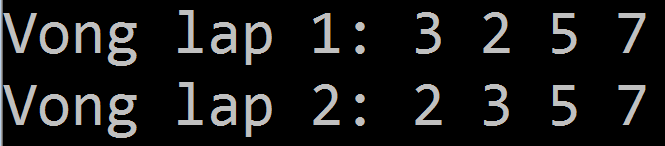Một số thuật toán sắp xếp cơ bản. Quick Sort có phải là thuật toán sắp xếp nhanh nhất?
Bài đăng này đã không được cập nhật trong 6 năm
I. Mở đầu.
- Một bài toán thực tế là bạn cần quản lý một lớp học nào đó mà danh sách tên hoặc điểm số của các học sinh được sắp xếp không theo một thứ tự nào đó khiến cho bạn rất khó để quản lý chính vì vậy bài toán sắp xếp sẽ giúp chúng ta dễ dàng hơn trong việc quản lý một công việc gì đó.
- Sắp xếp là một trong những bài toán thực tế phổ biến nhất trong lập trình, nó giúp chúng ta sắp xếp một danh sách hoặc một mảng theo một thứ tự nào đó(thường là tăng dần hoặc giảm dần).
II. Một số thuật toán sắp xếp thường gặp.
1. Thuật toán sắp xếp nổi bọt (Bubble Sort)
-
Ý tưởng: Liên tục hoán đổi các phần tử liền kề nhau nếu chúng sai thứ tự cho đến khi dãy được sắp xếp.
-
Ví dụ minh họa
![]()
-
Mã code:
void swap(int *a,int *b){
int temp=*a;
*a=*b;
*b=temp;
}
void bubblesort(int arr[],int n){
for(int i=0; i<n-1; i++){
for(int j=0; j<n-i-1; j++){
if(arr[j]>arr[j+1]){
swap(&arr[j],&arr[j+1]);
}
}
}
}
-
Phân tích bài toán
- Giả sử cần sắp xếp dãy 5 3 2 7 theo thứ tự tăng dần.
![]()
vòng lặp 1:
[5 3 2 7] -> [3 5 2 7] , so sánh 5 và 3 thấy 3 nhỏ hơn 5 -> đổi chỗ 3 và 5.
[3 5 2 7] -> [3 2 5 7] , so sánh 5 và 2 thấy 2 nhỏ hơn 5 -> đổi chỗ 2 và 5.
[ 3 2 5 7] -> [3 2 5 7], 5 < 7 đúng -> không có gì thay đổi
-> kết thúc vòng lặp 1 ta được [3 2 5 7]
vòng lặp 2:
[3 2 5 7] ->[2 3 5 7] , so sánh 3 và 2 thấy 2 nhỏ hơn 3 -> đổi chỗ 2 và 3.
[2 3 5 7] ->[2 3 5 7]], 3 < 5 đúng -> không có gì thay đổi.
[2 3 5 7] -> [2 3 5 7] , 5 < 7 đúng -> không có gì thay đổi.
Đến đây ta thu được dãy đã sắp xếp nhưng thuật toán chưa dừng ở đó mà nó tiếp tục lặp.
vòng lặp 3:
[2 3 5 7] -> [2 3 5 7]
[2 3 5 7] -> [2 3 5 7]
[2 3 5 7] -> [2 3 5 7]
-
Độ phức tạp thuật toán:
Trường hợp tốt nhất: O(n)
Trường hợp xấu nhất: O(n*n)
2. Thuật toán sắp xếp chọn (Selection Sort)
-
Ý tưởng: Chọn phần từ nhỏ nhất (hoặc lớn nhất) trong dãy gồm n phần từ, đưa phần từ này về vị trí đầu tiên của dãy và không quan tâm đến phần tử này nữa. Tiếp tục tìm phần tử nhỏ nhất(hoặc lớn nhất) từ vị trí thứ 2 đến vị trí thứ n trong dãy n-1, đưa phần từ này về vị trí thứ 2. Lặp lại cho đến khi dẫy chỉ còn 1 phần tử.
-
Ví dụ minh họa
![]()
-
Mã code:
void swap(int *a,int *b){
int temp=*a;
*a=*b;
*b=temp;
}
void selectionsort(int arr[],int n){
int min_idx;
for(int i=0; i<n-1; i++){
min_idx=i;
for(int j=i+1; j<n; j++){
if(arr[j]<arr[min_idx])
min_idx=j;
}
swap(&arr[min_idx],&arr[i]);
}
}
-
Phân tích bài toán
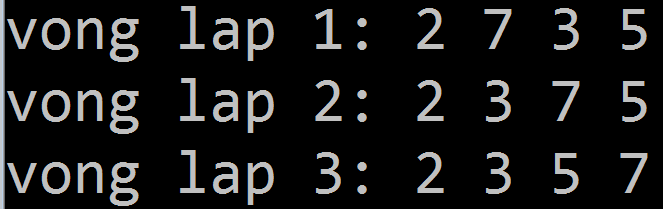
- Giả sử cần sắp xếp dãy 5 7 3 2 theo thứ tự tăng dần.
![]()
Vòng lặp 1:
[5 7 3 2] -> [2 7 3 5] , tìm được 2 là số nhỏ nhất ta đổi vị trí 2 cho 5
-> kết thúc vòng lặp 1 ta được [2 7 3 5]
Vòng lặp 2:
[2 7 3 5] -> [2 3 7 5], tìm được 3 là số nhỏ nhất trong dãy từ 2-n ta đổi chỗ 3 cho 7
-> kết thúc vòng lặp 2 ta được [2 3 7 5]
Vòng lặp 3:
[2 3 7 5] -> [2 3 5 7], tìm được 5 là số nhỏ nhất trong dãy từ 3-n ta đổi chỗ 5 cho 7
-> kết thúc vòng lặp 3 ta được [2 3 5 7]
Vòng lặp 3 cũng là vòng lặp cuối cùng vì dãy chỉ còn 1 phần tử thì n chắc chắn là lớn nhất, vậy ta đã thu được một dãy tăng dần với thuật toán sắp xếp chọn.
-
Độ phức tạp thuật toán:
Trường hợp tốt nhất: O(n*n)
Trường hợp xấu nhất: O(n*n)
3. Thuật toán sắp xếp nhanh (Quick Sort)
-
Ý tưởng: Quick sort là một thuật toán chia để trị nó chọn một phần tử trong mảng để làm điểm đánh dấu. Thuật toán sẽ thực hiện chia mảng thành các mảng con theo điểm mà mình đã chọn. Có nhiều cách chọn điểm khác nhau:
1. Luôn chọn phần tử đầu tiên 2. Luôn chọn phần tử cuối cùng 3. Chọn phần tử ngẫu nhiên 4. Chọn phần tử ở giữa![]()
-
Ví dụ minh họa
![]()
-
Mã code:
void swap(int *a,int *b){
int temp=*a;
*a=*b;
*b=temp;
}
int partition(int arr[],int l,int h){
int x=arr[h];
int i=l-1;
for(int j=l; j<=h-1; j++){
if(arr[j]<=x){
i++;
swap(&arr[i],&arr[j]);
}
}
swap(&arr[i+1],&arr[h]);
return(i+1);
}
void quicksort(int arr[],int l,int h){
if(l<h){
int p=partition(arr,l,h);
quicksort(arr,l,p-1);
quicksort(arr,p+1,h);
}
}
- Phân tích bài toán
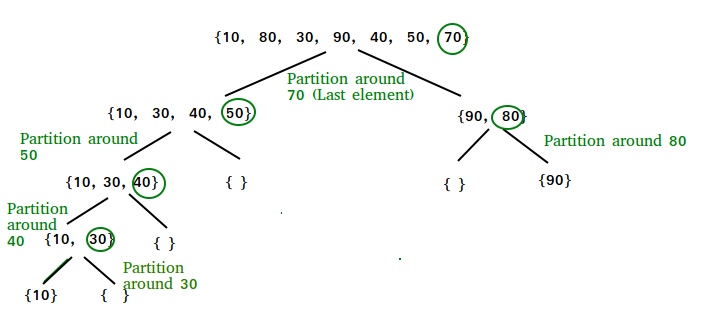
Xét mảng : arr[] = {10, 80, 30, 90, 40, 50, 70}
Ta chọn l = 0, h = 6, điểm chốt x = 70
Khởi tạo biến i = -1
Thực hiện lặp j = l -> h
j = 0: arr[j] (10) <= x (70) , biến i++ swap(arr[i] (10) , arr[j] (10) )
i = 0
Mảng vẫn chưa có gì thay đổi: arr[] = {10, 80, 30, 90, 40, 50, 70}
j = 1: arr[j] (80) > x (70) => biến i và mảng không đổi
j = 2: arr[j] (30) <= x(70) => biến i++ và swap(arr[i] (80) , arr[j] (30) )
i = 1
arr[] = {10, 30, 80, 90, 40, 50, 70}
j = 3: arr[j] (80) > 70 => biến i và mảng không đổi
j = 4: arr[j] (40)<= x(70), biến i++ và swap(arr[i] (80) , arr[j](40))
i = 2
arr[] = {10, 30, 40, 90, 80, 50, 70}
j = 5 : arr[j] (50) <= x (70) , biến i++ và swap(arr[i] (90) , arr[j] (50))
i = 3
arr[] = {10, 30, 40, 50, 80, 90, 70}
Thoát khỏi vòng lặp vì lúc này j = h-1
thực hiện swap(&arr[i+1](80),&arr[h](70))
arr[] = {10, 30, 40, 50, 70, 90, 80}
với hàm quicksort chúng sẽ thực hiện quicksort trái và quicksort phải
khi đó quicksort phải với điểm chốt x = 80
sau khi thực hiện sẽ thu được một dãy đã sắp xếp
arr[] = {10, 30, 40, 50, 70, 80, 90}
-
Độ phức tạp thuật toán
Trường hợp tốt nhất: O(nlog(n))
Trường hợp xấu nhất: O(n*n)
Vậy thuật toán quick sort có phải là thuật toán nhanh nhất không?
Thuật toán quick sort không phải là thuật toán sắp xếp nhanh nhất, tùy vào mỗi trường hợp đầu vào mà thuật toán sẽ có độ phức tạp khác nhau, trong những trường hợp đầu vào có thể là xấu nhất đối với quick sort thì độ phức tạp sẽ là O(n*n) bằng với những thuật toán sắp xếp khác nên không được coi là thuật toán sắp xếp nhanh nhất. Chính vì vậy dựa vào mỗi bài toán khác nhau mà người lập trình cần lựa chọn những thuật toán khác nhau sao cho bài toán được xử lý tối ưu nhất.
III. Kết luận
Thuật toán sắp xếp là một thuật toán rất hay được sử dụng trong khoa học máy tính. Nó giúp chúng ta tối ưu hóa việc sắp xếp một đồ vật, một danh sách...
Chính vì vậy không thể phủ nhận tầm quan trọng của thuật toán sắp xếp trong những bài toán thực tế mà lập trình viên cần giải quyết.
Ngoài những thuật toán sắp xếp ở trên còn rất nhiều thuật toán sắp xếp khác vô cùng hữu ích cho công việc lập trình của những lập trình viên trở nên dễ dàng hơn.
IV. Tham khảo
All rights reserved