2 x (-2) = -4, còn máy tính nghĩ sao? (Phần 2)
Bài đăng này đã không được cập nhật trong 6 năm
Trong phần trước của bài link, mình đã nêu về lịch sử hình thành của máy tính cũng như cấu tạo của máy tính. Cho những người chưa được bài trước thì trong phần đầu này mình tổng hợp lại nội dung trong bài trước.
- Máy tính có từ thời cổ, ban đầu rất thô sơ sau đó đến thời máy tính cơ khí. Cuối cùng là máy tính hiện đại như ngày nay.
- Máy tính được cấu tạo từ các linh kiện điện tử như: CPU, RAM, GPU ... Chi tiết hơn nữa là được cấu tạo từ các cổng logic: AND, OR, XOR, ...
- Các cổng logic kết hợp lại để thực hiện chức năng tính toán.
Do máy tính được cấu tạo từ các linh kiện điện tử và chỉ hiểu các dãy nhị phân 0,1. Và các phép tính mà máy tính có thể thực hiện là: +, -, SHR (dịch bit phải), SHL (dịch bit trái). Các phép tính đã nêu không thấy có phép x (nhân), vậy lúc ta sử dụng máy tính để nhân ra kết quả thì máy tính làm cách nào. Về cơ bản là phép nhân là nhiều phép cộng kết hợp lại do đó máy tính có thể sử dụng các phép cộng để ra các phép nhân. Nhưng sử dụng cách đó thì quá cồng kềnh với lẽ đó các nhà thông thái đã cho ra đời thuật toán nhân có dấu mà các mạch phần cứng có thể thực hiện nó một một cách dễ dàng.
1. Thuật toán nhân không dấu
Thuật toán nhân không dấu được mô tả qua mã giả
C = 0
A = 0
M = Multiplicand
Q = Multiplier
count = n
while (count!=0):
if Q0 == 1:
C,A = A + M
SHR: C,A,Q
count = count - 1
print("Result: ", (A,Q))
Thuật toán được mô tả như sau:
- M là số bị nhân, số hạng đứng trước
- Q là số nhân, số hạng đứng sau
- C là bit nhớ, chỉ có 1 bit
- A một phần của kết quả
- Q0 là bit cuối cùng của Q, VD: Q = 11010 ---> Q0 = 1
Ban đầu C và A được gán bằng 0, M và Q là giá trị người dùng truyền, count là độ dài bit của Q.
Tiếp theo vào vòng lặp:
- Lặp cho đến khi count = 0 thì dừng.
- Kiểm tra bit cuối cùng của Q nếu bằng 1 thì:
- C,A = A + M
- Dịch phải 1 bit dãy bit: C,A,Q
- giảm biến count đi 1 đơn vị
- Kiểm tra bit cuối cùng của Q nếu bằng 1 thì:
Để hiểu thuật toán ta sẽ lấy 1 ví dụ cho đễ.
VD: 11 x 13
Đầu tiên ta chuyển hết về dạng nhị phân không có dấu. Sau đó gán: M = 11 = 1011, Q = 13 = 1101, count = 4, A = 0000, C = 0
Quy trình thực hiện cũng như kết quả được mô tả ở hình bên dưới.
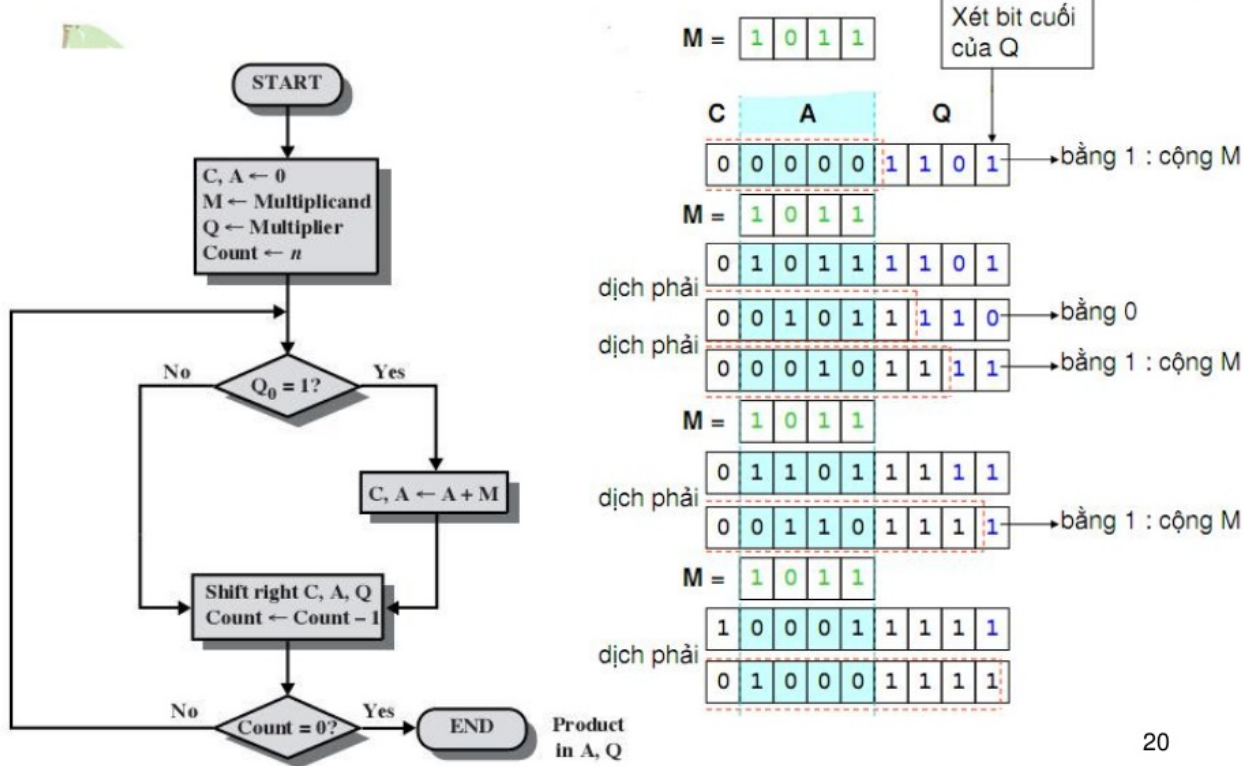
2. Thuật toán nhân có dấu Booth
Ở bên trên là thuật toán nhân không dấu, nhưng trong tính toán ta không chỉ nhân các số không dấu mà còn có cả số có dấu. Vì vậy, cũng là các nhà thông thái đã nghĩ ra thuật toán nhân có dấu để giải quyết vấn đề này.
Thuật toán nhân không dấu được mô tả qua mã giả.
A = 0
Q_1 = 0
M = Multiplicand
Q = Multiplier
count = n
while (count != 0):
if Q0,Q_1 == 01:
A = A + M
elif Q0,Q_1 == 10:
A = A - M
Arithmetic Shift Right: A,Q,Q_1
count = count - 1
print("Result: ", A,Q)
Thuật toán được mô tả như sau:
- A là một phần của kết quả, n bit
- là bit cuối cùng của Q, 1 bit
- là một bit được thêm vào, 1 bit
- M số bị nhân, n bit
- Q số nhân, n bit
- count độ dài bit
Khi khởi đầu thuật toán A, gán bằng, M và Q được truyền vào, count độ dài bit của Q
Tiếp theo là vòng lặp có điều kiện: dừng khi biến count = 0
- Kiểm tra 2 bit :
- Nếu bằng 01: A = A + M
- Nếu bằng 10: A = A - M
- Dịch phải toán học 1 bit dãy: A, Q, . Dịch phải toán học nghĩa là dịch phải và sao chép bit đầu tiên của A. VD: A = 1001 --> A = 1100
- Giảm count đi 1 đơn vị
Tiếp tục là ví dụ cho dễ hiểu
VD: -3 x 7
Cách đặt các biến và chi tiết cách thực hiện được mô tả qua hình.
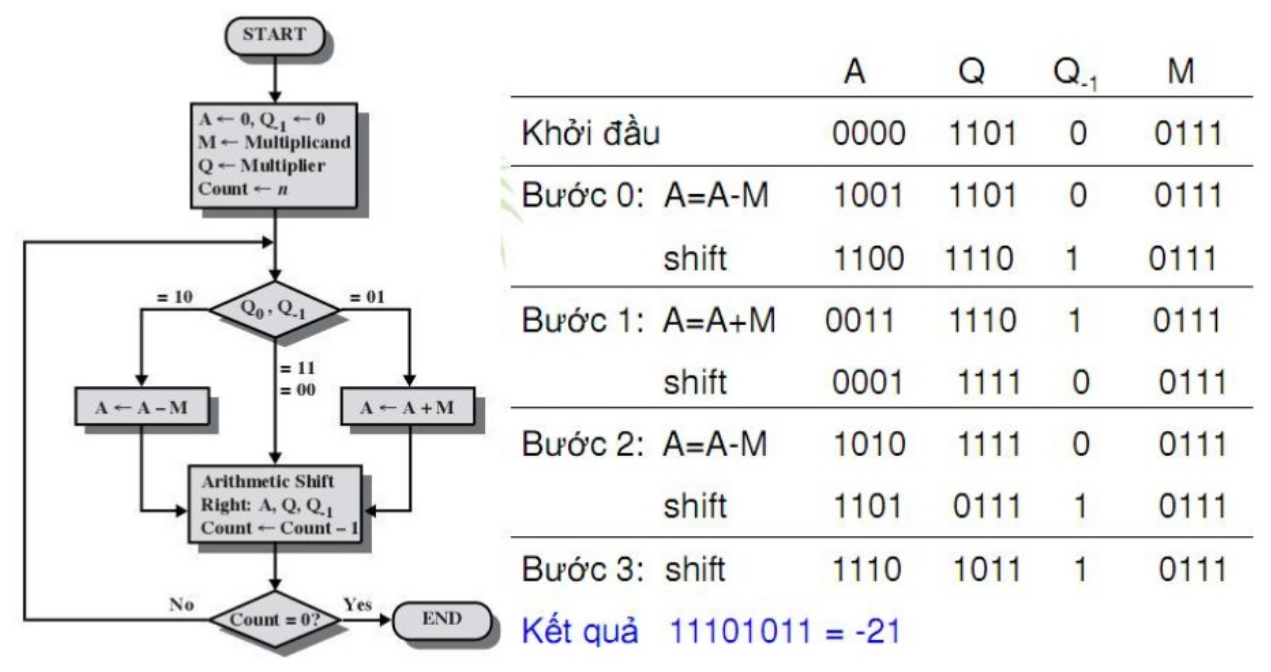
Đến đây cũng là kết thúc bài tìm hiểu cách thức tính toán của máy tính. Mong rằng qua bài sẽ cung cấp phần nào thông tin hữu ích cho bạn đọc 
All rights reserved
