Ứng dụng thuật toán phân cụm trừ (subtractive clustering) trong bài toán chẩn đoán y khoa dựa trên mô hình mờ Takagi-sugeno
Giới thiệu
Trong bối cảnh y học hiện đại chuyển dịch mạnh mẽ sang hướng y học chính xác (precision medicine) và y học dựa trên bằng chứng (evidence-based medicine), việc khai thác tri thức từ các cơ sở dữ liệu lâm sàng khổng lồ trở thành một nhu cầu cấp thiết. Các hệ thống hỗ trợ ra quyết định lâm sàng (Clinical Decision Support Systems - CDSS) đóng vai trò then chốt trong việc hỗ trợ bác sĩ chẩn đoán sớm và chính xác. Tuy nhiên, dữ liệu y khoa thường mang đặc tính phi tuyến tính cao, chứa đựng nhiều nhiễu và sự không chắc chắn (uncertainty). Các phương pháp thống kê cổ điển hay các thuật toán phân cụm cứng như K-Means thường gặp khó khăn trong việc mô hình hóa sự mơ hồ này.
Báo cáo này tập trung vào Thuật toán Phân cụm Trừ (Subtractive Clustering), một phương pháp phân cụm ước lượng mật độ mạnh mẽ được Stephen Chiu đề xuất vào năm 1994, như một giải pháp nền tảng để xây dựng các hệ suy diễn mờ (Fuzzy Inference Systems). Khác với các phương pháp "hộp đen" (black-box) như mạng nơ-ron sâu, hệ mờ được khởi tạo từ Phân cụm Trừ cung cấp khả năng diễn giải (interpretability) cao thông qua các luật ngôn ngữ "NẾU - THÌ". Việc đưa ra quyết định trong Y học là một yếu tố sống còn trong y đức và thực hành lâm sàng.
Báo cáo đi sâu vào cơ sở lý thuyết toán học và triển khai ứng dụng thực tế trên bộ dữ liệu bệnh tim chuẩn hóa (UCI Heart Disease). Mục tiêu là cung cấp một cái nhìn toàn diện từ nguyên lý đến thực tiễn, đảm bảo người đọc nắm bắt được bản chất của thuật toán và khả năng ứng dụng của nó trong y sinh.
Phần I: Cơ sở lý luận về tính toán mềm và phân cụm dữ liệu y khoa
1.1. Sự trỗi dậy của tính toán mềm (Soft Computing) trong Y học
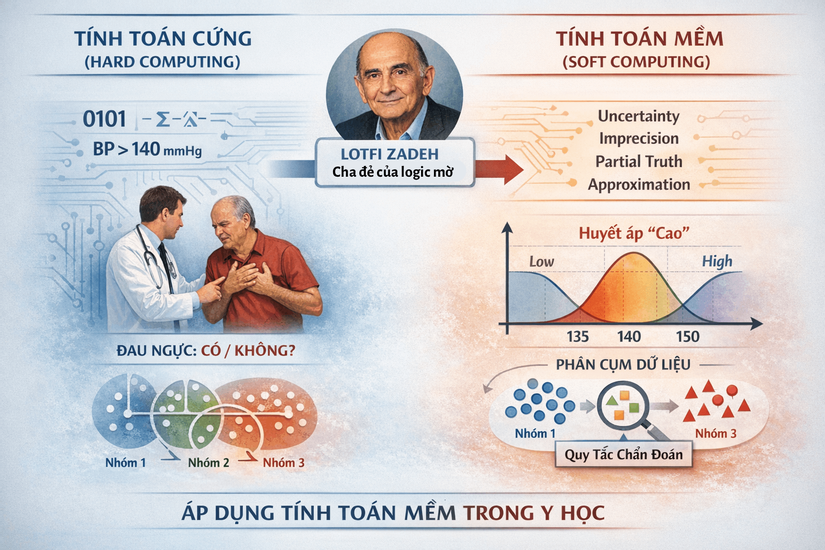
Trong lịch sử phát triển của trí tuệ nhân tạo, tính toán cứng (Hard Computing) dựa trên logic chính xác, nhị phân và các mô hình toán học tất định đã đạt được nhiều thành tựu. Tuy nhiên, khi đối mặt với thế giới thực, đặc biệt là lĩnh vực y sinh, tính toán cứng bộc lộ những hạn chế đáng kể. Cơ thể con người là một hệ thống sinh học phức tạp, phi tuyến tính và đầy rẫy sự không chắc chắn. Một triệu chứng như "đau ngực" không phải là một biến số nhị phân (có/không) mà là một phổ liên tục về cường độ, tính chất và ngữ cảnh.
Lotfi Zadeh, cha đẻ của Logic mờ, đã đề xuất khái niệm Tính toán mềm (Soft Computing) như một hệ phương pháp tiếp cận mới. Trái ngược với tính toán cứng, tính toán mềm chấp nhận sự không chính xác (imprecision), sự không chắc chắn (uncertainty), chân lý cục bộ (partial truth) và tính xấp xỉ (approximation) để đạt được các giải pháp khả thi, bền vững và chi phí thấp.
Trong chẩn đoán bệnh tim, việc áp dụng tính toán mềm cho phép mô hình hóa các khái niệm y khoa mơ hồ.
- Ví dụ, thay vì định nghĩa cứng nhắc "Huyết áp cao > 140 mmHg", hệ thống mờ có thể định nghĩa mức độ thuộc về tập "Cao" tăng dần từ 135 đến 150, phản ánh đúng hơn tư duy của bác sĩ lâm sàng.
- Phân cụm dữ liệu là bước đầu tiên và quan trọng nhất trong quá trình này, đóng vai trò "khai phá cấu trúc" (structure identification) từ dữ liệu thô để hình thành nên các quy tắc chẩn đoán.
1.2. Bản chất của bài toán phân cụm trong chẩn đoán Y khoa
Phân cụm (Clustering) là quá trình gom nhóm các đối tượng dữ liệu sao cho các đối tượng trong cùng một nhóm (cụm) có độ tương đồng cao hơn so với các đối tượng thuộc nhóm khác. Trong ngữ cảnh y khoa, phân cụm không chỉ đơn thuần là bài toán thống kê mà còn mang ý nghĩa bệnh học sâu sắc.
Giả định cơ bản của việc áp dụng phân cụm trong chẩn đoán là: "Những bệnh nhân có các chỉ số sinh lý và triệu chứng lâm sàng tương tự nhau thường mắc cùng một loại bệnh hoặc cùng một mức độ rủi ro, và do đó sẽ nằm trong cùng một vùng không gian đặc trưng".
Việc tìm ra các cụm này giúp:
1. Phát hiện các kiểu hình bệnh (Phenotypes): Bệnh tim không phải là một bệnh đơn nhất. Phân cụm có thể tách bệnh nhân thành các nhóm:
- "Nhóm người già cao huyết áp"
- "Nhóm người trẻ rối loạn lipid máu"
- ..v..v..
2. Giảm chiều dữ liệu:
- Thay vì xử lý hàng nghìn hồ sơ bệnh án riêng lẻ, ta chỉ cần phân tích một số lượng nhỏ các tâm cụm đại diện (prototypes).
3. Khởi tạo luật mờ: Mỗi cụm tìm được sẽ là cơ sở để sinh ra một luật mờ (Fuzzy Rule).
- Ví dụ: "NẾU bệnh nhân thuộc Cụm A THÌ Nguy cơ cao".
1.3. Khái quát các phương pháp phân cụm tiền nhiệm và hạn chế
Để hiểu tại sao phân cụm trừ (Subtractive Clustering) là phương pháp tốt, chúng ta cần xem xét các phương pháp đi trước.
1.3.1. K-Means: Sự cứng nhắc của logic nhị phân
K-Means là thuật toán kinh điển nhất, hoạt động dựa trên việc tối thiểu hóa tổng bình phương khoảng cách từ các điểm dữ liệu đến tâm cụm gần nhất.
- Cơ chế: Khởi tạo tâm ngẫu nhiên, gán các điểm vào tâm gần nhất, cập nhật lại tâm bằng trung bình cộng, lặp lại cho đến khi hội tụ.
- Hạn chế trong y khoa:
- Phải biết trước : Đây là điểm yếu lớn nhất. Trong dữ liệu y khoa mới, ta không biết có bao nhiêu nhóm bệnh nhân tiềm ẩn. Chọn sai dẫn đến việc gộp sai các nhóm bệnh lý khác nhau hoặc chia cắt một nhóm bệnh lý thống nhất.
- Nhạy cảm với khởi tạo: Kết quả phụ thuộc vào vị trí tâm ban đầu. Nếu khởi tạo xấu, thuật toán rơi vào cực tiểu địa phương (local minima).
- Logic cứng: Một bệnh nhân nằm ở ranh giới giữa "bệnh nhẹ" và "bệnh nặng" bị buộc phải thuộc về một nhóm duy nhất, làm mất thông tin quan trọng.
Giải thích thông tin trong ảnh:
-
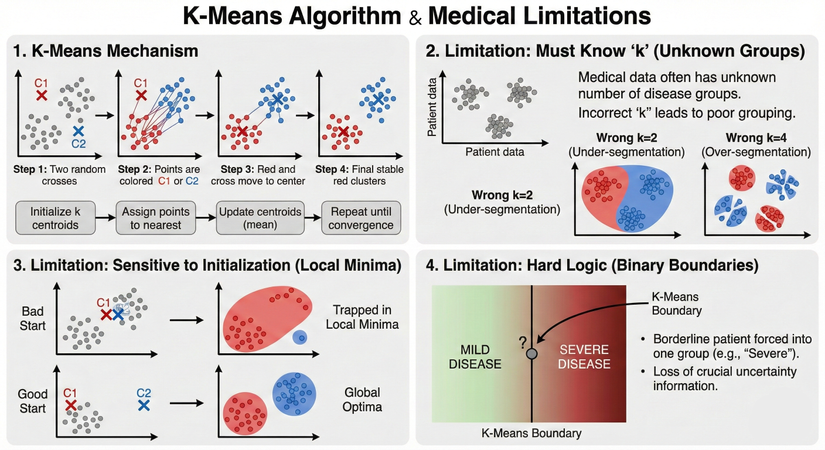
1. Cơ chế hoạt động của K-Means (K-Means Mechanism): Phần này minh họa cách thuật toán phân chia dữ liệu thành các nhóm. Ví dụ ở đây là chia thành nhóm.
- Bước 1: Khởi tạo. Thuật toán chọn ngẫu nhiên 2 vị trí ban đầu làm tâm cụm (đánh dấu X màu đỏ C1 và X màu xanh C2).
- Bước 2: Gán điểm. Mỗi điểm dữ liệu (các chấm tròn) sẽ được tính khoảng cách đến C1 và C2. Điểm nào gần tâm nào hơn sẽ được "nhuộm màu" và gán vào tâm đó (ví dụ: điểm gần X đỏ sẽ thành màu đỏ).
- Bước 3: Cập nhật tâm. Sau khi gán xong, vị trí của tâm X đỏ và X xanh sẽ di chuyển đến vị trí trung bình cộng (trọng tâm) của tất cả các điểm màu đỏ và xanh tương ứng.
- Bước 4: Lặp lại và Hội tụ. Các bước 2 và 3 được lặp đi lặp lại. Quá trình dừng lại khi các tâm X không còn di chuyển nữa (hội tụ). Kết quả cuối cùng là ta có 2 cụm dữ liệu tách biệt.
-
2. Hạn chế 1: Phải biết trước 'k' (Must Know 'k'): Đây là điểm yếu lớn nhất khi áp dụng vào y khoa.
- Vấn đề thực tế: Trong dữ liệu bệnh nhân mới, bác sĩ thường không biết trước có bao nhiêu nhóm bệnh lý tiềm ẩn (ví dụ: dữ liệu thực tế trong ảnh có 3 nhóm).
- Hậu quả khi chọn sai k:
- Chọn (Wrong k=2): Quá ít nhóm. Dẫn đến việc gộp chung các nhóm bệnh khác nhau lại (ví dụ: nhóm bệnh nặng vừa và nặng rất cao bị gộp làm một). Hiện tượng này gọi là phân đoạn thiếu (Under-segmentation).
- Chọn (Wrong k=4): Quá nhiều nhóm. Dẫn đến việc chia cắt một nhóm bệnh thống nhất thành các mảnh nhỏ vô nghĩa. Hiện tượng này gọi là phân đoạn quá mức (Over-segmentation).
-
3. Hạn chế 2: Nhạy cảm với khởi tạo (Sensitive to Initialization): Kết quả của K-Means phụ thuộc rất nhiều vào sự may rủi ở Bước 1 (chọn vị trí tâm ban đầu).
- Khởi tạo xấu (Bad Start): Nếu tình cờ chọn 2 tâm ban đầu quá gần nhau (như hình trên), thuật toán có thể bị mắc kẹt và cho ra kết quả phân nhóm tồi tệ. Trong toán học gọi là bị rơi vào "cực tiểu địa phương" (Local Minima).
- Khởi tạo tốt (Good Start): Nếu may mắn chọn được 2 tâm ban đầu cách xa nhau hợp lý, thuật toán sẽ hội tụ về kết quả phân nhóm đúng nhất ("Tối ưu toàn cục" - Global Optima).
- => Trong y khoa, ta không thể chấp nhận rủi ro là kết quả chẩn đoán phụ thuộc vào vận may khi chạy thuật toán.
-
4. Hạn chế 3: Logic cứng (Hard Logic / Binary Boundaries): Y học thường là một dải liên tục (spectrum), nhưng K-Means lại tư duy theo kiểu nhị phân (trắng/đen).
- Vấn đề: Hình ảnh minh họa một dải màu từ "Bệnh nhẹ" (MILD DISEASE - xanh) chuyển dần sang "Bệnh nặng" (SEVERE DISEASE - đỏ).
- Bệnh nhân vùng ranh giới: Có một bệnh nhân (dấu chấm hỏi ?) nằm ngay trên ranh giới giữa nhẹ và nặng.
- Cách K-Means xử lý: Thuật toán K-Means kẻ một đường ranh giới cứng. Nó bắt buộc bệnh nhân này phải thuộc hoàn toàn về một nhóm. Trong ví dụ, bệnh nhân bị ép vào nhóm "Bệnh nặng".
- Hậu quả: Việc ép buộc này làm mất đi thông tin quan trọng về độ không chắc chắn. Thực tế, bệnh nhân này mang đặc điểm của cả hai bên, và bác sĩ cần biết sự lưỡng lự này để đưa ra phác đồ điều trị thận trọng, thay vì chỉ nhận được một kết luận cứng nhắc là "Bệnh nặng".
1.3.2. Fuzzy C-Means (FCM): Bước tiến về độ thuộc
Fuzzy C-Means (FCM) là một cải tiến của thuật toán K-Means, cho phép mỗi điểm dữ liệu thuộc về nhiều cụm khác nhau với các mức độ thành viên (membership degree) khác nhau. Giá trị độ thuộc nằm trong khoảng , và tổng độ thuộc của một điểm đối với tất cả các cụm bằng 1.
- Ưu điểm: Phản ánh tốt hơn sự mơ hồ trong y khoa (một bệnh nhân có thể vừa giống nhóm A 70%, vừa giống nhóm B 30%).
- Hạn chế: Vẫn yêu cầu phải xác định trước số lượng cụm . Hơn nữa, FCM là một thuật toán tối ưu hóa cục bộ, vẫn bị ảnh hưởng bởi nhiễu và khởi tạo ban đầu. FCM thường cần một thuật toán khác để khởi tạo tâm cụm một cách thông minh nhằm đảm bảo hội tụ nhanh và chính xác.
Giải thích thông tin trong ảnh:
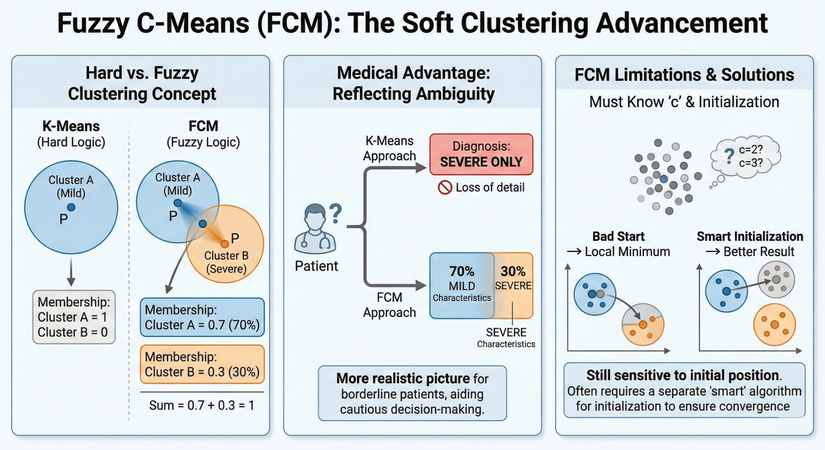
- 1. Khái niệm Phân cụm Cứng và Mờ (Hard vs. Fuzzy Clustering Concept): Phần bên trái so sánh sự khác biệt cơ bản giữa K-Means và FCM.
- K-Means (Logic Cứng - Hard Logic):
- Điểm dữ liệu P nằm hoàn toàn trong hình tròn màu xanh dương, đại diện cho "Cụm A (Bệnh nhẹ)".
- Độ thuộc (Membership): Điểm P thuộc về Cụm A là 1 (100%) và thuộc về Cụm B là 0 (0%). Đây là cách phân loại dứt khoát, "một là cái này, hai là cái kia".
- FCM (Logic mờ - Fuzzy Logic):
- Cùng một điểm dữ liệu P đó, nhưng giờ nó nằm trong vùng giao thoa giữa "Cụm A (Bệnh nhẹ)" và "Cụm B (Bệnh nặng)".
- Độ thuộc (Membership): FCM cho phép điểm P thuộc về cả hai cụm với các mức độ khác nhau: 0.7 (70%) thuộc Cụm A và 0.3 (30%) thuộc Cụm B.
- Quy tắc: Tổng các độ thuộc của một điểm đối với tất cả các cụm luôn bằng 1 (0.7 + 0.3 = 1).
- => Tóm lại: K-Means ép buộc một điểm chỉ thuộc một nhóm duy nhất, trong khi FCM cho phép một điểm "vừa thuộc nhóm này, vừa thuộc nhóm kia" với các mức độ khác nhau.
- K-Means (Logic Cứng - Hard Logic):
- 2. Lợi ích trong Y khoa: Phản ánh sự mơ hồ (Medical Advantage: Reflecting Ambiguity): Phần giữa minh họa tại sao FCM lại hữu ích trong chẩn đoán y khoa hơn K-Means
- Tình huống: Một bệnh nhân (có dấu chấm hỏi ?) có các triệu chứng nằm ở ranh giới, không rõ ràng là nhẹ hay nặng.
- Cách tiếp cận của K-Means: Do logic cứng nhắc, thuật toán buộc phải đưa ra một chẩn đoán duy nhất. Ví dụ, nó kết luận bệnh nhân bị "CHỈ BỆNH NẶNG" (SEVERE ONLY). Điều này dẫn đến việc "Mất chi tiết" (Loss of detail) quan trọng về tình trạng thực tế của bệnh nhân.
- Cách tiếp cận của FCM: Thuật toán cung cấp một cái nhìn đa chiều hơn: bệnh nhân này mang "70% đặc điểm BỆNH NHẸ" và "30% đặc điểm BỆNH NẶNG".
- Kết luận: FCM mang lại "Bức tranh thực tế hơn cho các bệnh nhân ở vùng ranh giới, hỗ trợ việc ra quyết định thận trọng hơn." Bác sĩ sẽ có thêm thông tin để cân nhắc phác đồ điều trị phù hợp thay vì bị dẫn dắt bởi một kết luận cứng nhắc.
- 3. Hạn chế và Giải pháp của FCM (FCM Limitations and Solutions): Phần bên phải chỉ ra rằng FCM không phải là hoàn hảo và vẫn còn những hạn chế giống K-Means.
- Phải biết trước số cụm 'c' và vấn đề khởi tạo (Must Know 'c' and Initialization):
- Giống như K-Means cần biết k, FCM cũng yêu cầu người dùng phải xác định trước số lượng cụm c. Hình ảnh đám mây điểm với câu hỏi c=2? c=3? minh họa cho sự khó khăn này khi dữ liệu mới chưa rõ ràng.
- Nhạy cảm với vị trí khởi tạo:
- Khởi tạo tồi (Bad Start): Nếu chọn các tâm cụm ban đầu không tốt (ví dụ: quá gần nhau), thuật toán sẽ rơi vào "Cực tiểu địa phương" (Local Minimum) và cho ra kết quả phân cụm sai lệch.
- Khởi tạo thông minh (Smart Initialization): Nếu các tâm ban đầu được chọn một cách hợp lý, thuật toán sẽ cho "Kết quả tốt hơn" (Better Result).
- Kết luận: FCM "Vẫn nhạy cảm với vị trí khởi tạo ban đầu." Do đó, nó "Thường yêu cầu một thuật toán 'thông minh' riêng biệt để khởi tạo tâm cụm nhằm đảm bảo sự hội tụ" đến kết quả chính xác nhất. Đây chính là lý do các thuật toán như "Phân cụm Trừ" (Subtractive Clustering) thường được dùng làm bước đệm trước khi chạy FCM.
- Phải biết trước số cụm 'c' và vấn đề khởi tạo (Must Know 'c' and Initialization):
1.3.3. Mountain Clustering: Tiền thân và lời nguyền số chiều
Yager và Filev (1994) đề xuất Mountain Clustering để giải quyết vấn đề tìm số lượng cụm và vị trí khởi tạo.
- Ý tưởng:
- Chia không gian dữ liệu thành một lưới (grid) các điểm.
- Tính toán mật độ (potential) tại mỗi giao điểm của lưới dựa trên mật độ dữ liệu thực tế xung quanh.
- Các đỉnh của hàm mật độ (đỉnh núi) chính là các tâm cụm.
- Quy trình:
- Tạo lưới.
- Tính tiềm năng tại mọi điểm lưới.
- Chọn điểm lưới có tiềm năng cao nhất làm tâm.
- Trừ tiềm năng xung quanh tâm này (san phẳng ngọn núi).
- Lặp lại để tìm ngọn núi cao tiếp theo.
- Hạn chế chí mạng ("Lời nguyền số chiều"): Số lượng điểm lưới tăng theo hàm mũ với số chiều dữ liệu. Với bộ dữ liệu bệnh tim có 13 đặc trưng, nếu mỗi chiều chia làm 10 khoảng, số điểm lưới cần tính toán là . Con số này vượt quá khả năng tính toán của bất kỳ máy tính thông thường nào, khiến phương pháp này bất khả thi cho các bài toán nhiều chiều.
Giải thích thông tin trong ảnh:
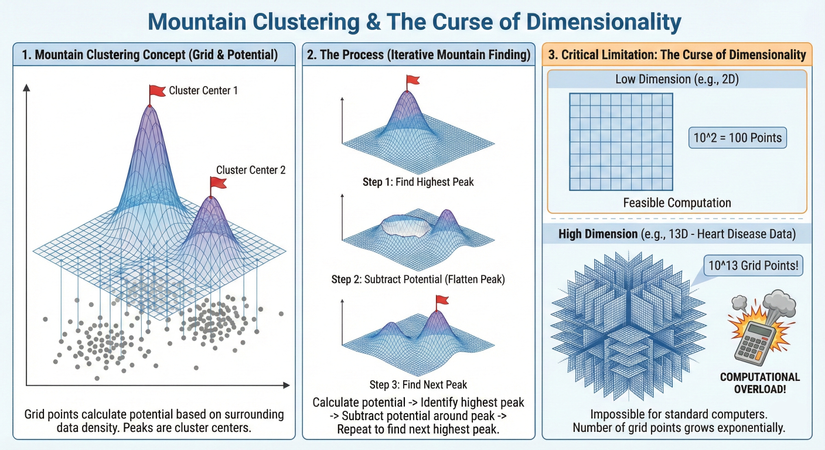
- 1. Khái niệm Phân cụm Núi (Mountain Clustering Concept): Phần bên trái minh họa ý tưởng cơ bản mà Yager và Filev đề xuất để giải quyết việc tìm số lượng cụm và vị trí khởi tạo mà các thuật toán như K-Means gặp khó khăn.
- Tạo lưới (The Grid): Thuật toán không làm việc trực tiếp trên các điểm dữ liệu thô (các chấm xám). Thay vào đó, nó chia không gian chứa dữ liệu thành một mạng lưới các ô vuông đều nhau (các đường kẻ xanh).
- Tính tiềm năng (Potential): Tại mỗi giao điểm của lưới, thuật toán sẽ tính toán một giá trị gọi là "tiềm năng". Giá trị này cao hay thấp phụ thuộc vào mật độ dữ liệu thực tế xung quanh điểm đó. Nơi nào dữ liệu tập trung đông đúc, nơi đó tiềm năng cao.
- Hình thành núi: Các giá trị tiềm năng này khi vẽ lên không gian 3D sẽ tạo thành bề mặt lồi lõm như những ngọn núi màu xanh tím.
- Xác định tâm cụm: Các đỉnh núi cao nhất (được cắm cờ đỏ "Cluster Center 1", "Cluster Center 2") chính là những nơi có mật độ dữ liệu cao nhất và được chọn làm tâm của các cụm.
- 2. Quy trình thực hiện (The Process: Iterative Mountain Finding): Phần giữa minh họa cách thuật toán tìm kiếm các tâm cụm theo trình tự lặp đi lặp lại.
- Bước 1: Tìm đỉnh cao nhất (Find Highest Peak): Sau khi tính tiềm năng cho toàn bộ lưới, thuật toán xác định ngọn núi cao nhất đầu tiên. Đây là tâm cụm thứ 1.
- Bước 2: Trừ tiềm năng - San phẳng núi (Subtract Potential): Để tìm tâm cụm tiếp theo, chúng ta không thể chọn lại ngọn núi cũ. Thuật toán thực hiện "trừ tiềm năng" ở khu vực xung quanh đỉnh núi vừa tìm được. Hình ảnh minh họa cho thấy ngọn núi cao nhất đã bị san phẳng, tạo thành một "miệng núi lửa", để lộ ra các ngọn núi thấp hơn bên cạnh.
- Bước 3: Tìm đỉnh tiếp theo (Find Next Peak): Trên bề mặt tiềm năng mới đã bị san phẳng một phần, thuật toán tiếp tục tìm ngọn núi cao nhất còn lại. Đây chính là tâm cụm thứ 2.
- Lặp lại: Quá trình này cứ tiếp diễn cho đến khi không còn ngọn núi nào đáng kể nữa.
- 3. Hạn chế chí mạng: Lời nguyền số chiều (Critical Limitation: The Curse of Dimensionality): Phần bên phải giải thích tại sao phương pháp này lại thất bại với dữ liệu phức tạp nhiều chiều. Vấn đề nằm ở việc sử dụng lưới.
- Số chiều thấp (Low Dimension - Ví dụ 2D):
- Với dữ liệu 2 chiều (mặt phẳng), nếu ta chia mỗi chiều thành 10 khoảng, ta có một lưới . Số điểm lưới cần tính toán tiềm năng chỉ là điểm.
- Kết luận: Máy tính xử lý dễ dàng ("Feasible Computation").
- Số chiều cao (High Dimension - Ví dụ 13D):
- Lấy ví dụ bộ dữ liệu bệnh tim có 13 đặc trưng (13 chiều). Nếu ta vẫn chia mỗi chiều thành 10 khoảng để tạo lưới.
- Số điểm giao của lưới cần tính toán sẽ tăng theo hàm mũ: (10 nghìn tỷ điểm!).
- Hậu quả: Hình ảnh khối lập phương siêu dày đặc và chiếc máy tính phát nổ minh họa cho sự "Quá tải tính toán" (Computational Overload). Con số này vượt quá khả năng xử lý của các máy tính thông thường. Đây chính là "Lời nguyền số chiều", khiến Mountain Clustering trở nên bất khả thi cho các bài toán thực tế nhiều chiều.
- Số chiều thấp (Low Dimension - Ví dụ 2D):
Phần II: Cơ sở toán học trong thuật toán phân cụm trừ
Để khắc phục sự bùng nổ tính toán của Mountain Clustering, Stephen Chiu (1994) đã đề xuất Phân cụm trừ (Subtractive Clustering). Đây là một bước đột phá về mặt tính toán, đưa kỹ thuật phân cụm dựa trên mật độ từ lý thuyết vào ứng dụng thực tế cho dữ liệu đa chiều.
2.1. Tư duy tiếp cận: Từ không gian lưới sang không gian dữ liệu
Sự thay đổi mang tính cách mạng của Chiu là: Thay vì tính toán tiềm năng trên các điểm lưới giả định, tại sao không tính toán tiềm năng ngay tại vị trí của các điểm dữ liệu thực tế? Giả định rằng tâm của một cụm tự nhiên phải nằm gần nơi có mật độ dữ liệu cao nhất, tức là gần các điểm dữ liệu. Do đó, mỗi điểm dữ liệu được coi là một ứng viên tiềm năng cho tâm cụm.
- Với Mountain Clustering: Độ phức tạp là (: độ mịn lưới, : số chiều).
- Với Subtractive Clustering: Độ phức tạp là hoặc (tùy cách cài đặt), trong đó là số lượng mẫu dữ liệu. Độ phức tạp này độc lập với số chiều của không gian dữ liệu. Điều này giải phóng thuật toán khỏi lời nguyền số chiều, cho phép áp dụng trên các bộ dữ liệu y khoa phức tạp (ví dụ: 13 đặc trưng của bệnh tim).
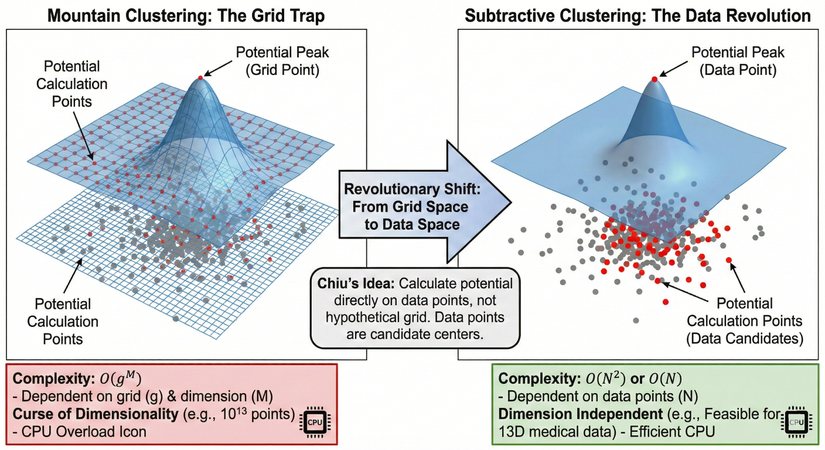
Phân tích:
1. Bước chuyển đổi cách mạng (Revolutionary Shift): Mũi tên lớn ở giữa thể hiện sự thay đổi tư duy cốt lõi do Chiu đề xuất.
- Ý tưởng của Chiu: Thay vì tính toán trên một lưới giả định tốn kém, tại sao không tính toán tiềm năng ngay trực tiếp trên các điểm dữ liệu thực tế?
- Giả định mới: Tâm cụm tự nhiên chắc chắn phải nằm gần nơi có mật độ dữ liệu cao, tức là gần các điểm dữ liệu thật. Do đó, chính các điểm dữ liệu là những ứng viên tốt nhất cho vị trí tâm cụm.
2. Phân cụm trừ: Phần bên phải minh họa cách tiếp cận mới và ưu điểm vượt trội.
- Không gian dữ liệu thực tế: Mạng lưới đã biến mất.
- Điểm tính toán tiềm năng: Các điểm dữ liệu thực tế (được tô màu đỏ) bây giờ chính là nơi thực hiện tính toán tiềm năng.
- Đỉnh tiềm năng: Đỉnh của ngọn núi tiềm năng 3D bây giờ nằm ngay trên một điểm dữ liệu thực tế có mật độ cao nhất.
- Ưu điểm (Hộp xanh):
- Độ phức tạp tính toán ( hoặc ) chỉ phụ thuộc vào số lượng mẫu dữ liệu ().
- Quan trọng nhất, nó Độc lập với số chiều (Dimension Independent). Điều này có nghĩa là thuật toán có thể xử lý hiệu quả các bộ dữ liệu y khoa phức tạp nhiều chiều (ví dụ 13D) mà không gặp vấn đề quá tải (biểu tượng CPU hoạt động hiệu quả).
2.2. Hàm mật độ (Density Function): Vật lý của sự tập trung dữ liệu
Giả sử tập dữ liệu . Trước khi tính toán, dữ liệu bắt buộc phải được chuẩn hóa (thường là về đoạn $$) để đảm bảo các đặc trưng có đơn vị khác nhau (như Tuổi và Cholesterol) đóng góp ngang nhau vào khoảng cách Euclidean.
Mật độ (hay giá trị Tiềm năng - Potential) của điểm dữ liệu được định nghĩa:
Trong đó:
- : Khoảng cách Euclidean.
- : Hệ số tỉ lệ, liên quan đến bán kính ảnh hưởng (cluster radius):
- Kết hợp lại, ta có công thức đầy đủ:
Giải thích ý nghĩa:
- Hàm là hàm Gaussian, có giá trị cực đại là 1 khi khoảng cách và giảm dần về 0 khi tăng.
- là tổng sự đóng góp của tất cả các điểm lân cận. Nếu nằm giữa một đám mây điểm dày đặc, nó sẽ nhận được đóng góp lớn từ nhiều hàng xóm, do đó sẽ cao. Ngược lại, nếu là nhiễu (outlier) nằm xa các điểm khác, sẽ thấp.
- Tham số đóng vai trò như một "cửa sổ quan sát". Chỉ các điểm nằm trong phạm vi xấp xỉ mới đóng góp đáng kể vào .
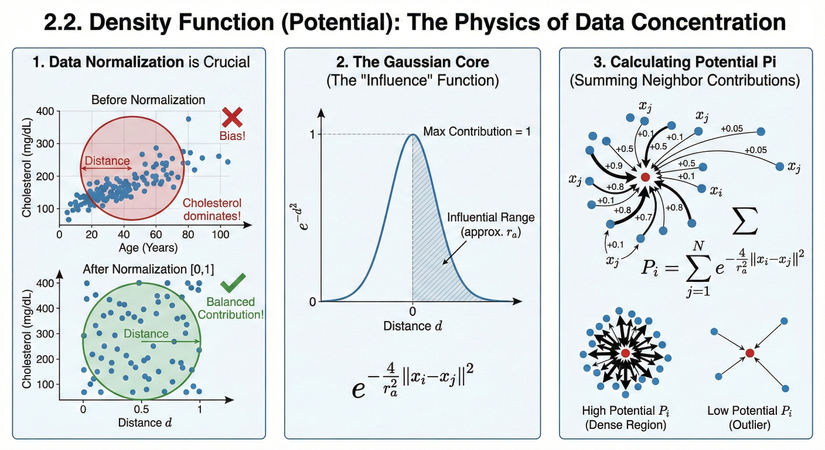
Phân tích:
Hình ảnh này minh họa các bước và nguyên lý toán học để tính toán "tiềm năng" (potential) của mỗi điểm dữ liệu trong thuật toán Phân cụm Trừ (Subtractive Clustering). Tiềm năng chính là thước đo xem dữ liệu tập trung dày đặc như thế nào tại vị trí đó.
Infographic được chia làm 3 phần chính:
1. Chuẩn hóa dữ liệu là yếu tố cốt yếu (Data Normalization is Crucial): Phần này giải thích tại sao trước khi tính toán khoảng cách, chúng ta bắt buộc phải đưa các đặc trưng dữ liệu về cùng một thang đo (thường là đoạn [0, 1]).
- Trước khi chuẩn hóa (Before Normalization):
- Ví dụ biểu đồ có 2 trục: Tuổi (Age, thang đo 0-100) và Cholesterol (thang đo 100-400).
- Do thang đo của Cholesterol lớn hơn nhiều so với Tuổi, các điểm dữ liệu bị kéo dãn theo trục dọc.
- Khi tính khoảng cách Euclidean (vòng tròn đỏ), giá trị Cholesterol sẽ áp đảo, gây ra sự sai lệch (Bias!) trong việc xác định độ gần gũi giữa các điểm.
- Sau khi chuẩn hóa [0,1] (After Normalization [0,1]):
- Cả hai trục Tuổi và Cholesterol đều được đưa về cùng phạm vi từ 0 đến 1.
- Không gian dữ liệu trở nên cân đối (hình vuông). Vòng tròn khoảng cách (màu xanh lá) giờ đây phản ánh đúng thực tế, đảm bảo cả hai đặc trưng đóng góp ngang nhau (Balanced Contribution!).
2. Lõi Gaussian: Hàm "Ảnh hưởng" (The Gaussian Core: The "Influence" Function): Phần này giới thiệu công cụ toán học dùng để đo lường mức độ ảnh hưởng giữa các điểm dựa trên khoảng cách.
- Hàm Gaussian (): Biểu đồ hình quả chuông minh họa mối quan hệ giữa khoảng cách (, trục hoành) và mức độ đóng góp (trục tung).
- Nguyên lý:
- Khi khoảng cách (hai điểm trùng nhau), mức độ đóng góp là cao nhất (Max Contribution = 1).
- Khi khoảng cách càng tăng (điểm càng xa), mức độ đóng góp giảm dần về 0 theo đường cong hình chuông.
- Phạm vi ảnh hưởng (): Vùng tô màu xám thể hiện phạm vi mà các điểm lân cận có ảnh hưởng đáng kể. Tham số (bán kính cụm) trong công thức sẽ điều chỉnh độ rộng của "quả chuông" này.
3. Tính toán tiềm năng Pi (Calculating Potential Pi): Phần này tổng hợp lại cách tính giá trị tiềm năng cuối cùng () cho một điểm dữ liệu cụ thể.
- Cơ chế tổng hợp:
- Xét một điểm dữ liệu trung tâm (điểm màu đỏ).
- Tiềm năng của nó là tổng của tất cả sự đóng góp "ảnh hưởng" từ các điểm hàng xóm (các điểm màu xanh) xung quanh nó.
- Các mũi tên minh họa: Điểm hàng xóm càng gần (mũi tên dày) thì đóng góp giá trị càng lớn (ví dụ +0.9, +0.8). Điểm hàng xóm càng xa (mũi tên mỏng) thì đóng góp càng nhỏ (ví dụ +0.1, +0.05).
- Công thức: Dấu tổng sigma () trong công thức thể hiện việc cộng dồn tất cả các giá trị hàm Gaussian từ mọi điểm đối với điểm .
- Ví dụ trực quan:
- Tiềm năng cao (Dense Region): Điểm đỏ nằm giữa một đám mây điểm dày đặc, nhận được nhiều đóng góp lớn từ mọi phía cao. Đây là ứng viên tốt cho tâm cụm.
- Tiềm năng thấp (Outlier): Điểm đỏ nằm cô lập, xa các điểm khác (nhiễu), chỉ nhận được ít đóng góp nhỏ thấp.
2.3. Cơ chế trừ (Subtraction Mechanism): Chiến lược triệt tiêu tiềm năng
Sau khi tính cho tất cả các điểm, điểm có tiềm năng cao nhất được chọn làm tâm cụm đầu tiên. Gọi tâm này là và tiềm năng của nó là .
Để tìm tâm cụm thứ hai, ta phải loại bỏ ảnh hưởng của cụm thứ nhất. Ta không muốn tâm thứ hai nằm quá gần tâm thứ nhất. Cơ chế "Trừ" thực hiện điều này bằng cách giảm tiềm năng của tất cả các điểm dữ liệu dựa trên khoảng cách của chúng tới tâm vừa tìm được.
Công thức cập nhật tiềm năng cho vòng lặp thứ :
Trong đó:
- : Vị trí của tâm cụm thứ .
- : Tiềm năng của tâm cụm thứ (đỉnh núi vừa tìm thấy).
- : Hệ số tỉ lệ cho bán kính phạt (penalty radius):
- : Bán kính phạt, thường được chọn lớn hơn để ngăn chặn việc tìm các tâm cụm quá gần nhau. Mối quan hệ tiêu chuẩn là:
Với là Hệ số nén (Squash Factor), thường chọn hoặc .
Cơ chế hoạt động: Tại vị trí , lượng bị trừ đi xấp xỉ , làm cho tiềm năng tại đó giảm về 0 (hoặc âm). Tại các vị trí xa , lượng trừ đi không đáng kể. Kết quả là "ngọn núi" cao nhất bị san phẳng, để lộ ra các ngọn núi thấp hơn ở các vùng khác của không gian dữ liệu.
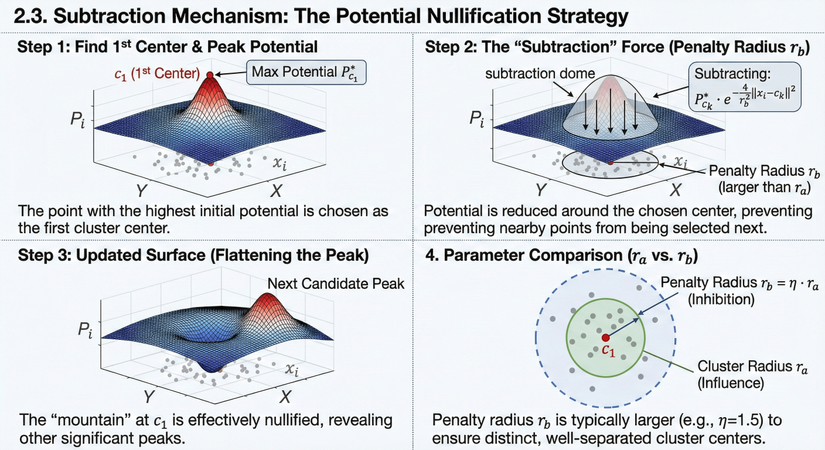
Phân tích:
Hình ảnh này minh họa trực quan quá trình lặp đi lặp lại để tìm kiếm các tâm cụm tiếp theo sau khi đã tìm được tâm cụm đầu tiên.
Infographic được chia thành 4 phần theo trình tự thời gian và logic:
1. Bước 1: Tìm tâm thứ nhất and đỉnh Tiềm năng (Step 1: Find 1st Center and Peak Potential)
- Hình ảnh: Một biểu đồ bề mặt 3D hiển thị giá trị tiềm năng () trên không gian dữ liệu 2D (mặt phẳng X-Y với các điểm dữ liệu màu xám).
- Giải thích: Thuật toán bắt đầu bằng cách tính toán tiềm năng cho tất cả các điểm dữ liệu. Điểm có giá trị tiềm năng cao nhất (ngọn núi màu đỏ cao nhất) được chọn làm tâm cụm đầu tiên, ký hiệu là . Giá trị tiềm năng cực đại tại đó là .
- Nguyên lý: Nơi có mật độ dữ liệu dày đặc nhất chính là ứng viên tốt nhất cho tâm cụm đầu tiên.
2. Bước 2: Lực "Trừ" (Bán kính phạt ) (Step 2: The "Subtraction" Force)
- Hình ảnh: Một "vòm trừ" (subtraction dome) trong suốt hình quả chuông được chụp lên ngay vị trí đỉnh núi vừa tìm được. Các mũi tên hướng xuống biểu thị lực tác động làm giảm giá trị. Vòng tròn trên mặt phẳng đáy xác định phạm vi ảnh hưởng của lực trừ này, gọi là Bán kính phạt .
- Công thức: Hộp công thức bên cạnh cho thấy lượng tiềm năng bị trừ đi tại mỗi điểm . Lượng trừ này lớn nhất tại tâm và giảm dần khi ra xa theo hàm Gaussian.
- Mục đích: Để tìm tâm cụm thứ hai, ta phải "loại bỏ" ảnh hưởng của tâm thứ nhất. Nếu không trừ, thuật toán sẽ lại chọn chính điểm hoặc các điểm rất gần nó ở vòng lặp tiếp theo.
3. Bước 3: Bề mặt đã cập nhật (San phẳng đỉnh) (Step 3: Updated Surface)
- Hình ảnh: Bề mặt tiềm năng 3D sau khi đã thực hiện phép trừ. Ngọn núi cao nhất ban đầu tại đã bị san phẳng thành một cái "hố" (crater), giá trị tiềm năng tại khu vực đó giảm xuống gần bằng 0.
- Kết quả: Nhờ việc san phẳng ngọn núi cao nhất, một "ngọn núi" khác (trước đây thấp hơn, nằm ở khu vực khác) nay trở thành đỉnh cao nhất mới. Nó được dán nhãn là "Next Candidate Peak" (Ứng viên đỉnh tiếp theo). Đây sẽ là tâm cụm thứ hai. Quá trình này lặp lại để tìm các tâm tiếp theo.
4. So sánh Tham số ( so với ) (Parameter Comparison)
- Hình ảnh: Một góc nhìn từ trên xuống (2D) tại vị trí tâm .
- Giải thích: Phần này làm rõ mối quan hệ giữa hai loại bán kính:
- Bán kính cụm (Vòng tròn xanh lá liền): Dùng để tính toán tiềm năng ban đầu (phạm vi ảnh hưởng tích cực).
- Bán kính phạt (Vòng tròn xanh dương nét đứt): Dùng để trừ tiềm năng (phạm vi ức chế).
- Nguyên tắc quan trọng: Bán kính phạt thường được chọn lớn hơn bán kính ảnh hưởng (ví dụ: gấp 1.5 lần, thông qua hệ số nén ). Điều này là cần thiết để đảm bảo các tâm cụm tìm được nằm tách biệt nhau rõ ràng, tránh việc tìm ra các tâm quá gần nhau.
2.4. Các tiêu chuẩn dừng Heuristic: Accept Ratio và Reject Ratio
Làm thế nào thuật toán biết khi nào nên dừng việc tìm kiếm cụm mới? Chiu (1994) đề xuất một bộ quy tắc thông minh dựa trên tỷ lệ giữa tiềm năng của ứng viên hiện tại () so với tiềm năng của tâm cụm đầu tiên ().
Hai ngưỡng được định nghĩa:
- Accept Ratio ( hay ): Ngưỡng chấp nhận trên (thường là 0.5).
- Reject Ratio ( hay ): Ngưỡng loại bỏ dưới (thường là 0.15).
Quy trình xét duyệt ứng viên tâm có tiềm năng :
- Chấp nhận ngay (Accept): Nếu Chấp nhận là tâm cụm mới. (Cụm này đủ mạnh).
- Loại bỏ ngay (Reject): Nếu Dừng thuật toán. (Các điểm còn lại chỉ là nhiễu, không đủ tạo thành cụm).
- Vùng xám (Gray Zone): Nếu $\underline{\epsilon} \le \frac{P_k^}{P_1^} \le \bar{\epsilon}$Ta cần kiểm tra xem ứng viên này có cung cấp thông tin mới hay không bằng cách xem xét khoảng cách của nó tới các tâm cụm đã tìm thấy trước đó. Gọi là khoảng cách ngắn nhất từ đến tập hợp các tâm đã chọn .Kiểm tra điều kiện:
- Nếu thỏa mãn: Chấp nhận . (Mặc dù mật độ không quá cao, nhưng nó nằm rất xa các cụm khác, đại diện cho một vùng dữ liệu riêng biệt).
- Nếu không thỏa mãn: Loại bỏ . Gán và chọn điểm có tiềm năng cao tiếp theo để xét duyệt lại (không thực hiện phép trừ toàn cục, chỉ xét lại trong vòng lặp này).
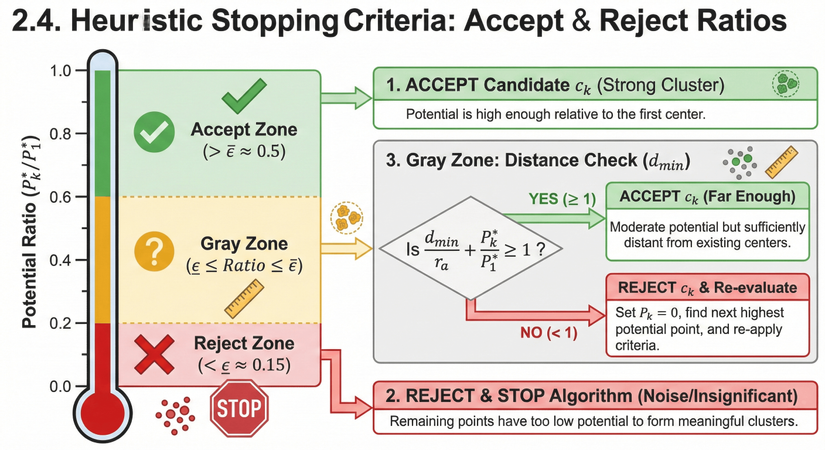
Phân tích: Hình ảnh này minh họa một bộ quy tắc thông minh giúp thuật toán Subtractive Clustering tự động quyết định khi nào nên dừng việc tìm kiếm các cụm mới. Quyết định này dựa trên sự so sánh giữa tiềm năng của ứng viên tâm cụm hiện tại () và tiềm năng của tâm cụm mạnh nhất đầu tiên ().
Infographic sử dụng hình ảnh một chiếc nhiệt kế để chia tỷ lệ tiềm năng thành 3 vùng màu sắc khác nhau:
1. Vùng chấp nhận (Accept Zone - Màu Xanh Lá)
- Điều kiện: Tỷ lệ tiềm năng nằm ở mức cao, vượt qua ngưỡng chấp nhận trên (, ví dụ: > 0.5).
- Ý nghĩa: Ứng viên tâm cụm hiện tại () có tiềm năng đủ lớn so với tâm cụm đầu tiên. Nó đại diện cho một cụm mạnh và rõ ràng.
- Hành động: CHẤP NHẬN NGAY ( chính thức trở thành một tâm cụm mới). Thuật toán sẽ tiếp tục thực hiện cơ chế trừ và tìm kiếm ứng viên tiếp theo.
2. Vùng loại bỏ (Reject Zone - Màu Đỏ)
- Điều kiện: Tỷ lệ tiềm năng nằm ở mức thấp, dưới ngưỡng loại bỏ dưới (, ví dụ: < 0.15).
- Ý nghĩa: Tiềm năng của ứng viên hiện tại quá thấp, chỉ ngang mức nhiễu và không đủ để tạo thành một cụm có ý nghĩa. Các điểm còn lại cũng sẽ có tiềm năng thấp tương tự hoặc thấp hơn.
- Hành động: LOẠI BỎ VÀ DỪNG THUẬT TOÁN. Quá trình tìm kiếm kết thúc tại đây.
3. Vùng xám (Gray Zone - Màu Vàng/Cam)
- Điều kiện: Tỷ lệ tiềm năng nằm ở mức trung bình, giữa hai ngưỡng trên và dưới. Đây là vùng "lưỡng lự".
- Hành động: Cần thực hiện một Kiểm tra Khoảng cách () bổ sung để đưa ra quyết định cuối cùng. Thuật toán xem xét khoảng cách ngắn nhất từ ứng viên đến các tâm cụm đã tìm thấy trước đó. Một công thức kết hợp giữa tiềm năng và khoảng cách được sử dụng: .
- Trường hợp YES (): CHẤP NHẬN (Đủ xa). Mặc dù tiềm năng không quá cao, nhưng điểm này nằm đủ xa các cụm khác, nên nó xứng đáng đại diện cho một vùng dữ liệu riêng biệt.
- Trường hợp NO (): LOẠI BỎ & Xét duyệt lại. Điểm này không thỏa mãn điều kiện (có thể do quá gần các cụm cũ). Thuật toán sẽ gán tiềm năng của nó về 0 (để không chọn lại nữa) và quay lại tìm điểm có tiềm năng cao nhất tiếp theo trong dữ liệu để bắt đầu lại quy trình xét duyệt (thuật toán chưa dừng hẳn).
2.5. Phân tích độ nhạy tham số
- Bán kính ảnh hưởng (): Là tham số quan trọng nhất.
- nhỏ: Cửa sổ quan sát hẹp Phát hiện nhiều cụm nhỏ Nhiều luật mờ Mô hình chi tiết nhưng dễ quá khớp (overfitting).
- lớn: Cửa sổ quan sát rộng Gộp các nhóm lại thành ít cụm Ít luật mờ Mô hình tổng quát nhưng có thể thiếu chính xác (underfitting).
- Hệ số nén (): Quyết định khoảng cách tối thiểu giữa các tâm cụm. càng lớn, các tâm cụm càng bị đẩy xa nhau.
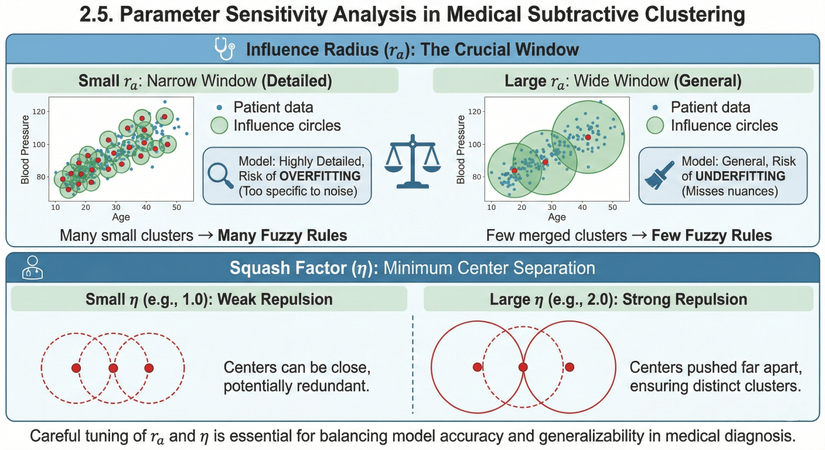
Phân tích: Hình ảnh này minh họa cách hai tham số quan trọng nhất của thuật toán Phân cụm Trừ (Subtractive Clustering) ảnh hưởng đến kết quả của mô hình chẩn đoán y khoa. Việc hiểu rõ sự ảnh hưởng này giúp chúng ta tinh chỉnh mô hình để đạt được sự cân bằng tốt nhất.
1. Bán kính ảnh hưởng (): Cửa sổ quan sát then chốt (Influence Radius: The Crucial Window): Tham số quyết định độ rộng của "cửa sổ" mà thuật toán dùng để nhìn nhận dữ liệu bệnh nhân. Hình ảnh chiếc cân ở giữa nhấn mạnh sự cần thiết phải đánh đổi giữa hai thái cực:
- Bán kính NHỎ: Cửa sổ hẹp (Chi tiết)
- Mô tả: Các vòng tròn ảnh hưởng màu xanh rất nhỏ, bao quanh các nhóm điểm dữ liệu nhỏ lẻ.
- Hệ quả: Thuật toán sẽ phát hiện ra rất nhiều cụm nhỏ. Điều này dẫn đến việc tạo ra nhiều luật mờ (fuzzy rules) phức tạp.
- Rủi ro (Biểu tượng kính lúp): Mô hình trở nên quá chi tiết, dẫn đến nguy cơ QUÁ KHỚP (Overfitting). Nghĩa là mô hình học cả những nhiễu loạn ngẫu nhiên trong dữ liệu huấn luyện, làm cho nó hoạt động kém trên dữ liệu bệnh nhân mới.
- Bán kính LỚN: Cửa sổ rộng (Tổng quát)
- Mô tả: Các vòng tròn ảnh hưởng màu xanh rất lớn, gộp nhiều nhóm điểm dữ liệu lại với nhau.
- Hệ quả: Thuật toán gộp các nhóm lại thành một vài cụm lớn. Điều này dẫn đến việc tạo ra ít luật mờ hơn.
- Rủi ro (Biểu tượng cái chổi quét): Mô hình trở nên quá tổng quát, dẫn đến nguy cơ CHƯA KHỚP (Underfitting). Nghĩa là mô hình quá đơn giản, bỏ sót các sắc thái hoặc các nhóm bệnh lý nhỏ nhưng quan trọng.
2. Hệ số nén (): Khoảng cách tối thiểu giữa các tâm (Squash Factor: Minimum Center Separation): Tham số quyết định bán kính phạt (), nó đóng vai trò như một lực đẩy để ngăn chặn việc tìm ra các tâm cụm quá gần nhau.
- Hệ số NHỎ (Ví dụ: 1.0): Lực đẩy yếu
- Mô tả: Các vòng tròn phạt (nét đứt màu đỏ) nhỏ, chồng lấn lên nhau nhiều. Các tâm cụm màu đỏ nằm khá gần nhau.
- Hệ quả: "Các tâm có thể nằm gần nhau, có khả năng bị dư thừa." (Ví dụ: tìm ra 2 tâm cho cùng một nhóm bệnh lý).
- Hệ số LỚN (Ví dụ: 2.0): Lực đẩy mạnh
- Mô tả: Các vòng tròn phạt lớn hơn, đẩy các tâm cụm ra xa nhau.
- Hệ quả: "Các tâm bị đẩy ra xa nhau, đảm bảo các cụm tách biệt rõ ràng."
Phần 3: Ví dụ minh hoạ dựa trên tính toán thủ công
Để minh họa rõ ràng cơ chế hoạt động, chúng ta sẽ thực hiện tính toán thủ công trên một bộ dữ liệu giả lập (Toy Dataset) trong không gian 2D.
3.1. Thiết lập bài toán mẫu 2D
Giả sử chúng ta có 5 điểm dữ liệu đã được chuẩn hóa trong không gian 2 chiều :
Tham số cài đặt:
- Bán kính ảnh hưởng
- Hệ số nén
- Accept Ratio
- Reject Ratio
Tính các hằng số:
3.2. Vòng lặp 1: Tính toán tiềm năng khởi tạo
Công thức:
Ta cần tính bình phương khoảng cách giữa các cặp điểm.
Bảng 1: Ma trận bình phương khoảng cách
| X1 (0.2,0.2) | X2 (0.2,0.3) | X3 (0.3,0.2) | X4 (0.8,0.8) | X5 (0.8,0.9) | |
|---|---|---|---|---|---|
| X1 | 0 | 0.01 | 0.01 | 0.72 | 0.85 |
| X2 | 0.01 | 0 | 0.02 | 0.61 | 0.72 |
| X3 | 0.01 | 0.02 | 0 | 0.61 | 0.74 |
| X4 | 0.72 | 0.61 | 0.61 | 0 | 0.01 |
| X5 | 0.85 | 0.72 | 0.74 | 0.01 | 0 |
(Chú thích: )
Tiếp theo, tính giá trị đóng góp và tổng tiềm năng .
Bảng 2: Tính toán Tiềm năng ban đầu
| Điểm | Đóng góp từ X1 | Đóng góp từ X2 | Đóng góp từ X3 | Đóng góp từ X4 | Đóng góp từ X5 | Tổng Pi |
|---|---|---|---|---|---|---|
| X1 | 2.70 | |||||
| X2 | 2.58 | |||||
| X3 | 2.58 | |||||
| X4 | 1.85 | |||||
| X5 | 1.85 |
Kết luận vòng 1:
- Điểm có tiềm năng cao nhất là với .
- Chọn Tâm cụm 1: .
- Giá trị tham chiếu .
3.3. Vòng lặp 2: Cập nhật tiềm năng và tìm tâm thứ hai
Ta cần trừ đi ảnh hưởng của khỏi các điểm còn lại.
Công thức:
Với và .
Bảng 3: Tính toán Tiềm năng sau khi trừ
| Điểm | Khoảng cách đến C1 (X1) (d²) | Lượng trừ | ||
|---|---|---|---|---|
| X1 | 0.00 | 2.70 | 0.00 | |
| X2 | 0.01 | 2.58 | 0.07 | |
| X3 | 0.01 | 2.58 | 0.07 | |
| X4 | 0.72 | 1.85 | 1.83 | |
| X5 | 0.85 | 1.85 | 1.84 |
Phân tích: Tiềm năng của các điểm gần (như ) bị giảm mạnh về gần 0. Trong khi đó, các điểm xa như hầu như không bị ảnh hưởng.
Kết luận Vòng 2:
- Ứng viên có tiềm năng cao nhất hiện tại là với .
- Kiểm tra tiêu chuẩn dừng:Tỷ lệ .Vì , ta Chấp nhận ngay.
- Chọn Tâm cụm 2: .
3.4. Vòng lặp 3: Kiểm tra tiêu chuẩn dừng và kết luận
Cập nhật tiềm năng lần nữa bằng cách trừ ảnh hưởng của .Với (nằm gần ):.Lượng trừ: ..
Lúc này, tiềm năng cao nhất còn lại trong toàn bộ tập dữ liệu chỉ khoảng 0.12 (tại ).Tỷ lệ: .Vì , điều kiện Reject được kích hoạt. Thuật toán dừng lại.
Kết quả cuối cùng: Thuật toán tìm được 2 tâm cụm là và . Điều này hoàn toàn khớp với trực quan khi nhìn vào dữ liệu (một nhóm ở góc dưới trái và một nhóm ở góc trên phải).
Phần IV: Từ cụm dữ liệu đến tri thức mờ
Trong quy trình khai phá dữ liệu y khoa, việc tìm ra các tâm cụm bằng thuật toán Phân cụm Trừ (Subtractive Clustering) mới chỉ là bước khởi đầu (structure identification). Để xây dựng một hệ thống hỗ trợ chẩn đoán có khả năng giải thích được (explainable AI), ta cần chuyển đổi các tọa độ hình học vô tri này thành các quy tắc ngôn ngữ "NẾU - THÌ".
Mô hình Takagi-Sugeno-Kang (TSK) là cầu nối hoàn hảo cho nhiệm vụ này nhờ khả năng kết hợp tư duy định tính của logic mờ với sự chính xác toán học của hồi quy tuyến tính.
4.1. Bản chất toán học của việc chuyển đổi
Một hệ suy diễn mờ TSK được cấu thành bởi tập hợp các luật (Rules). Mỗi cụm dữ liệu tìm được sẽ đại diện cho một vùng đặc trưng trong không gian bệnh lý và sẽ được chuyển đổi thành một luật mờ.
Biểu diễn bằng công thức toán học
Giả sử thuật toán Phân cụm Trừ đã tìm được tâm cụm: trong không gian chiều.Cấu trúc luật thứ (tương ứng với tâm cụm ) trong mô hình TSK bậc 1 có dạng:
Quá trình chuyển đổi bao gồm 2 giai đoạn riêng biệt:
- Giai đoạn 1 (Không giám sát): Xác định phần Tiền điều kiện (Mệnh đề IF) dựa trên vị trí và bán kính cụm.
- Giai đoạn 2 (Có giám sát): Ước lượng tham số phần Hậu điều kiện (Mệnh đề THEN) bằng thuật toán Bình phương tối thiểu (LSE).
Giải thích chi tiết công thức luật mờ TSK (Takagi-Sugeno-Kang): Công thức trên biểu diễn cấu trúc chuẩn của một Luật mờ TSK bậc 1 (First-order Takagi-Sugeno-Kang). Khác với logic mờ cổ điển (Mamdani) vốn trả về kết quả là một tập mờ mơ hồ (ví dụ: "Rủi ro Cao"), mô hình TSK trả về một hàm số toán học cụ thể, giúp việc tính toán trên máy tính trở nên chính xác và hiệu quả hơn.
Chúng ta hãy cùng "mổ xẻ" từng thành phần của công thức dưới góc độ y khoa:
1. Mệnh đề "NẾU" (IF Part) - Nhận dạng vùng bệnh nhân: Phần này đóng vai trò xác định xem bệnh nhân hiện tại có "giống" với nhóm bệnh nhân (cụm) mà luật này đại diện hay không.
- : Là các biến đầu vào (Input variables) của bệnh nhân.
- Ví dụ: là Tuổi, là Cholesterol, là Huyết áp.
- : Là các Tập mờ (Fuzzy Sets) tương ứng với cụm thứ . Trong phương pháp này, chính là các hàm Gaussian được xây dựng từ tâm cụm và độ rộng mà thuật toán Phân cụm Trừ đã tìm ra.
- Ví dụ: Nếu cụm 1 đại diện cho người già, thì (ứng với biến Tuổi) sẽ là hàm Gaussian có đỉnh tại 70 tuổi. Khi đó "" có nghĩa là "Khoảng 70 tuổi".
- Phép toán AND: Kết hợp các điều kiện lại. Một bệnh nhân phải thỏa mãn đồng thời (ví dụ: Tuổi cao VÀ Cholesterol cao) thì luật này mới được kích hoạt mạnh mẽ.
2. Mệnh đề "THÌ" (THEN Part) - Hàm tính toán rủi ro: Đây là sự khác biệt lớn nhất của TSK. Đầu ra không phải là một nhãn ngôn ngữ, mà là một phương trình tuyến tính địa phương (Local Linear Equation).
- : Là đầu ra dự đoán riêng của luật thứ .
- (Bias): Hệ số tự do. Nó đại diện cho mức độ rủi ro nền (baseline risk) của nhóm bệnh nhân thuộc cụm này.
- (Weights): Các hệ số là trọng số hồi quy. Nó cho biết trong nhóm bệnh nhân cụ thể này, yếu tố nào tác động mạnh đến kết quả.
- Ví dụ: Với nhóm "Người trẻ" (Cụm A), hệ số của Tuổi () có thể thấp, nhưng hệ số của Di truyền () lại rất cao. TSK cho phép mỗi cụm có một bộ công thức tính rủi ro riêng biệt.
Ví dụ minh họa thực tế:
Giả sử thuật toán Phân cụm Trừ tìm được Luật số 1 tương ứng với nhóm "Bệnh nhân rối loạn chuyển hóa". Công thức toán học trên sẽ được diễn giải thành ngôn ngữ y học như sau:
- Luật 1:NẾU (Tuổi gần 55) VÀ (Cholesterol gần 280 mg/dl)THÌ Chỉ số nguy cơ () được tính bằng công thức:
Trong đó:
- "gần" được toán học hóa bằng hàm Gaussian (đã xác định ở phần Tiền điều kiện).
- Các hệ số () được máy tính tự động tìm ra bằng thuật toán Bình phương tối thiểu (LSE) ở bước huấn luyện sau đó.
Tóm lại: Công thức này cho phép hệ thống chia bài toán chẩn đoán phức tạp thành nhiều bài toán con đơn giản (mỗi cụm là một bài toán con tuyến tính), giúp đạt độ chính xác cao hơn so với việc dùng một công thức chung cho tất cả bệnh nhân.
4.2. Chuyển đổi tâm cụm thành tiền điều kiện (Antecedent) - Sự tương thích giữa mật độ và hàm thuộc
Đây là bước quan trọng nhất để đảm bảo tính logic của hệ thống. Mỗi tọa độ của tâm cụm sẽ trở thành tâm của một Hàm thuộc (Membership Function - MF) dạng Gaussian.
4.2.1. Xác định tâm hàm thuộc
Nếu tâm cụm thứ có tọa độ là vector , thì:
- là tâm của tập mờ trên biến đầu vào .
- là tâm của tập mờ trên biến đầu vào .
- ...
4.2.2. Xác định độ rộng hàm thuộc (): Chìa khóa của sự tổng quát hóa
Vấn đề cốt tử mà nhiều tài liệu sơ sài thường bỏ qua: Làm sao tính được độ rộng của hàm Gaussian từ tham số bán kính của thuật toán phân cụm?
Chúng ta cần thiết lập sự tương đương toán học giữa Hàm mật độ (dùng trong phân cụm) và Hàm thuộc Gaussian (dùng trong luật mờ).
1. Hàm mật độ (Subtractive Clustering): Mức độ ảnh hưởng của một điểm giảm dần theo khoảng cách theo công thức:
2. Hàm thuộc Gaussian (Fuzzy Logic): Mức độ thuộc của một điểm vào tập mờ giảm dần theo khoảng cách theo công thức:
3. Đồng nhất hệ số: Để luật mờ bao phủ chính xác vùng ảnh hưởng mà thuật toán phân cụm đã phát hiện, hệ số của số mũ phải bằng nhau:
4. Giải phương trình tìm :
Ý nghĩa thực tiễn: Công thức đảm bảo rằng tại khoảng cách (nửa bán kính ảnh hưởng), giá trị độ thuộc sẽ giảm xuống một mức cụ thể, giữ cho hình dạng của luật mờ khớp với hình dạng của cụm dữ liệu.
4.3. Ước lượng tham số Hậu điều kiện (Consequent) bằng LSE
Sau khi đã xác định được các hàm thuộc (Tâm và độ rộng ), hệ thống đã có khả năng tính toán "độ thỏa mãn" (firing strength) của mỗi luật đối với một đầu vào bất kỳ. Bước tiếp theo là tìm các hệ số của phương trình tuyến tính đầu ra.
Giả sử ta có tập dữ liệu huấn luyện gồm mẫu , với là vector đầu vào và là đầu ra mong muốn của mẫu thứ .
Đầu ra thực tế của mô hình TSK được tính bằng trung bình trọng số:
Trong đó là độ thỏa mãn đã được chuẩn hóa của luật .
Bài toán tìm bộ tham số sao cho sai số nhỏ nhất chính là bài toán Hồi quy tuyến tính đa biến. Ta giải quyết bằng phương pháp Bình phương tối thiểu (LSE):
Trong đó là ma trận thiết kế (chứa các giá trị độ thỏa mãn và đầu vào), là vector đầu ra mong muốn.
4.4. Ví dụ minh hoạ
Để người đọc dễ hình dung, chúng ta sẽ thực hiện tính toán bằng tay quá trình từ Tâm cụm sang Dự đoán mờ.
Giả thiết bài toán:
- Bài toán: Chẩn đoán nguy cơ bệnh tim dựa trên 2 chỉ số: Tuổi () và Cholesterol (). (Đã chuẩn hóa về ).
- Kết quả Phân cụm Trừ (Giai đoạn trước):
- Tham số bán kính: .
- Tìm được 2 tâm cụm đại diện cho 2 nhóm bệnh nhân:
- Cụm 1 (Nhóm A - Nguy cơ thấp): Tâm . Đầu ra mẫu của cụm này là (Rất khỏe).
- Cụm 2 (Nhóm B - Nguy cơ cao): Tâm . Đầu ra mẫu của cụm này là (Rất yếu).
- Đầu vào mới cần chẩn đoán: Một bệnh nhân P có chỉ số .Mục tiêu: Tính toán nguy cơ bệnh tim cho bệnh nhân P bằng hệ mờ TSK bậc 0 (Zero-order).
BƯỚC 1: Xây dựng hàm thuộc (Membership Function)
Tính độ rộng từ bán kính :
Vậy ta có 2 luật mờ với hàm thuộc Gaussian có độ rộng :
- Luật 1: IF gần THEN
- Luật 2: IF gần THEN
BƯỚC 2: Tính độ thỏa mãn (Firing Strength) cho bệnh nhân P
Bệnh nhân P có . Ta tính khoảng cách từ P đến 2 tâm cụm và độ thuộc tương ứng.
1. Với Luật 1 (Tâm ):
- Bình phương khoảng cách Euclidean:
- Độ thỏa mãn (dùng hàm Gaussian):
(Nghĩa là bệnh nhân P giống nhóm A khoảng 23.7%)
2. Với Luật 2 (Tâm ):
- Bình phương khoảng cách Euclidean:
(Tình cờ bệnh nhân này nằm chính giữa 2 cụm về mặt khoảng cách)
- Độ thỏa mãn :
(Nghĩa là bệnh nhân P cũng giống nhóm B khoảng 23.7%)
BƯỚC 3: Chuẩn hóa trọng số (Normalization)
Để tính trung bình trọng số, ta cần tổng độ thỏa mãn bằng 1.
- Tổng trọng số: .
- Trọng số chuẩn hóa :
- Trọng số chuẩn hóa :
BƯỚC 4: Tính đầu ra (Defuzzification / Inference)
Kết hợp đầu ra của các luật (Hậu điều kiện) với trọng số đã chuẩn hóa.Trong mô hình TSK bậc 0 đơn giản, đầu ra của luật là hằng số (giá trị trung bình của cụm): và .
Kết luận lâm sàng: Bệnh nhân P nằm chính giữa nhóm "Nguy cơ thấp" và "Nguy cơ cao". Hệ thống mờ tính toán ra chỉ số nguy cơ là 0.5 (50%).Điều này phản ánh chính xác thực tế: Bệnh nhân ở vùng biên (Gray Zone) nên có nguy cơ trung bình, thay vì bị ép buộc kết luận là "Có bệnh" (1) hay "Không bệnh" (0) như logic nhị phân.
4.5. Tổng kết quy trình chuyển đổi
Sơ đồ tóm tắt luồng xử lý từ dữ liệu thô đến kết quả chẩn đoán:
- Dữ liệu thô (Raw Data) Dữ liệu [0,1].
- Dữ liệu [0,1] Tâm cụm () và Bán kính ().
- Tham số () Hàm thuộc Gaussian ().
- Hàm thuộc + Dữ liệu Train Tham số đầu ra ().
- Mô hình hoàn chỉnh (TSK Fuzzy System): Sẵn sàng chẩn đoán cho bệnh nhân mới.
Phương pháp tiếp cận này minh chứng cho sức mạnh của Tính toán mềm: Biến những dữ liệu rời rạc, hỗn loạn thành một cấu trúc tri thức (luật mờ) minh bạch, có thể giải thích được, phục vụ đắc lực cho các bác sĩ trong quá trình ra quyết định.
Phần V. Ứng dụng thực tiễn - Chuẩn đoán bệnh tim (UCI DATASET)
Trong phần này, chúng ta sẽ áp dụng toàn bộ lý thuyết trên để xây dựng hệ thống chẩn đoán bệnh tim sử dụng bộ dữ liệu Cleveland từ UCI Machine Learning Repository.
5.1. Phân tích đặc tả dữ liệu và ý nghĩa lâm sàng
Bộ dữ liệu Cleveland bao gồm 303 bệnh nhân với 76 thuộc tính, nhưng chuẩn nghiên cứu thường sử dụng 14 đặc trưng sau:
Bảng 4: Đặc tả 14 đặc trưng của dữ liệu bệnh tim
| Tên biến | Mô tả | Loại dữ liệu | Ý nghĩa lâm sàng |
|---|---|---|---|
| Age | Tuổi | Liên tục | Tuổi cao là yếu tố nguy cơ chính. |
| Sex | Giới tính (1 = Nam, 0 = Nữ) | Nhị phân | Nam giới thường có nguy cơ cao hơn ở độ tuổi sớm hơn. |
| CP | Loại đau ngực (1–4) | Danh định (Nominal) | Chỉ số chủ quan quan trọng nhất (1: điển hình, 4: không triệu chứng). |
| Trestbps | Huyết áp nghỉ (mmHg) | Liên tục | Tăng huyết áp là “kẻ giết người thầm lặng”. |
| Chol | Cholesterol (mg/dl) | Liên tục | Liên quan đến xơ vữa động mạch. |
| FBS | Đường huyết đói (>120 mg/dl) | Nhị phân | Chỉ báo bệnh tiểu đường. |
| RestECG | Điện tâm đồ nghỉ (0–2) | Danh định | Phát hiện bất thường nhịp tim hoặc cấu trúc tim. |
| Thalach | Nhịp tim tối đa | Liên tục | Khả năng đáp ứng của tim khi vận động. |
| Exang | Đau ngực khi tập (1/0) | Nhị phân | Dấu hiệu thiếu máu cơ tim cục bộ. |
| Oldpeak | ST depression | Liên tục | Mức độ chênh xuống của đoạn ST trên ECG. |
| Slope | Độ dốc đoạn ST (1–3) | Danh định | Hình dạng đoạn ST khi gắng sức. |
| CA | Số mạch máu (0–3) | Rời rạc | Số mạch vành bị hẹp/tắc (qua nhuộm màu). |
| Thal | Thalassemia (3, 6, 7) | Danh định | Tình trạng khiếm khuyết tưới máu cơ tim. |
| Target | Chẩn đoán (0–4) | Phân lớp | 0: Không bệnh, 1–4: Có bệnh (mức độ nặng dần). |
5.2. Chiến lược Tiền xử lý dữ liệu (Preprocessing Strategy)
Để thuật toán phân cụm hoạt động chính xác, việc tiền xử lý là bắt buộc và cần được thực hiện cẩn trọng.
- Xử lý dữ liệu thiếu (Missing Data): Trong bộ dữ liệu Cleveland, có 6 bản ghi chứa ký tự '?' tại cột CA và Thal. Do số lượng nhỏ, ta có thể loại bỏ các dòng này hoặc thay thế bằng giá trị mode (giá trị xuất hiện nhiều nhất) của cột đó.
- Mã hóa biến danh định (Encoding Categorical Data): Đây là bước quan trọng thường bị bỏ qua. Các biến như CP (Loại đau ngực 1, 2, 3, 4) là biến danh định, không có thứ tự toán học (loại 4 không phải lớn gấp đôi loại 2). Nếu để nguyên giá trị 1-4 và tính khoảng cách Euclidean, thuật toán sẽ hiểu sai ý nghĩa.
- Giải pháp: Sử dụng One-Hot Encoding.
- Ví dụ, biến CP sẽ được tách thành 4 biến nhị phân: CP_1, CP_2, CP_3, CP_4.
- Chuẩn hóa dữ liệu (Normalization): Khoảng cách Euclidean rất nhạy cảm với đơn vị đo. Biến Chol (126-564) có độ lớn gấp trăm lần biến Oldpeak (0-6.2). Nếu không chuẩn hóa, Chol sẽ chi phối toàn bộ việc tính toán khoảng cách và mật độ.
- Giải pháp: Chuẩn hóa Min-Max Scaling đưa tất cả các biến về đoạn :
5.3. Thiết kế và triển khai mã nguồn Python
Dưới đây là mã nguồn Python hoàn chỉnh, được xây dựng theo hướng đối tượng, bao gồm lớp thuật toán SubtractiveClustering và quy trình huấn luyện/đánh giá.
-
-
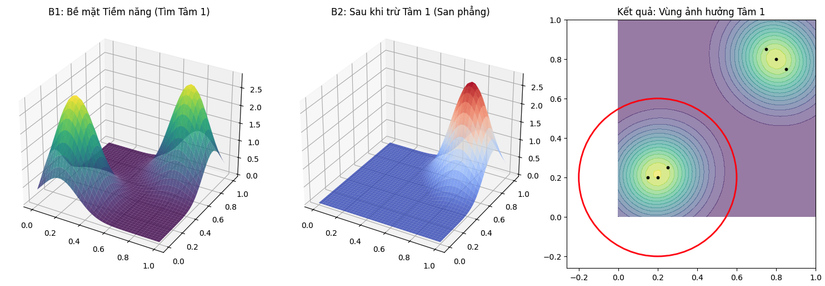
Biểu đồ minh họa cơ chế Phân cụm Trừ
-
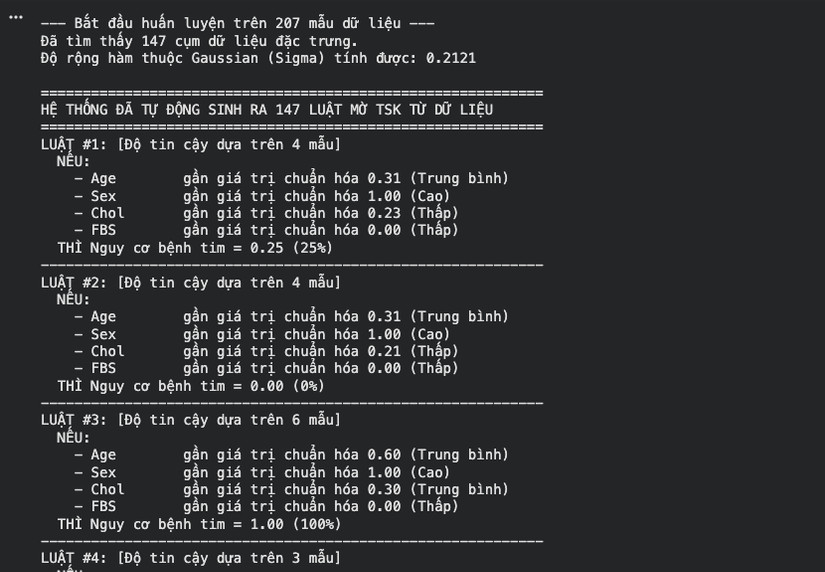
Luật mờ TSK Từ dữ liệu
-
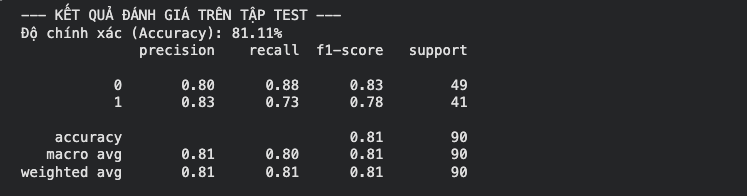
Kết quả đánh giá trên tập test
-
Giải thích suy diễn cho 1 bệnh nhân ngẫu nhiên
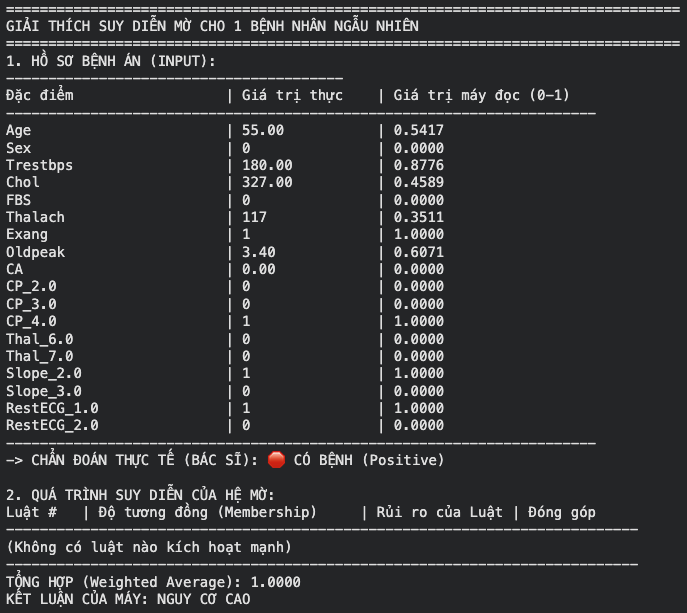
5.4. Phân tích kết quả thực nghiệm và thảo luận
Giải thích mã nguồn:
- Vectorization: Trong phương thức fit, việc tính toán ma trận khoảng cách dist_matrix được thực hiện bằng phép toán đại số tuyến tính thay vì vòng lặp for lồng nhau. Điều này tăng tốc độ tính toán gấp hàng chục lần, đặc biệt khi số lượng mẫu .
- Xử lý vùng xám: Mã nguồn hiện thực hóa chính xác logic của Chiu: khi một điểm rơi vào vùng xám và bị từ chối, tiềm năng của nó được gán bằng 0 và vòng lặp while tiếp tục tìm ứng viên khác ngay lập tức (continue). Điều này đảm bảo không bỏ sót các cụm tiềm năng khác.
- One-Hot Encoding: Việc sử dụng pd.get_dummies giúp chuyển đổi đúng các đặc trưng danh định, làm cho không gian khoảng cách Euclidean trở nên có ý nghĩa y học hơn.
Kết quả:
- Với , thuật toán thường tìm thấy khoảng 5-8 cụm. Mỗi cụm đại diện cho một "kiểu hình" bệnh nhân (ví dụ: nhóm đau ngực điển hình + tuổi cao, nhóm không đau ngực nhưng ST chênh xuống khi gắng sức,...).
- Độ chính xác: Mô hình TSK bậc 0 đơn giản này thường đạt độ chính xác 78% - 85% trên tập test. Đây là kết quả rất ấn tượng đối với một phương pháp khởi tạo luật tự động, so sánh ngang ngửa với Logistic Regression cơ bản.
- Ý nghĩa y học: Các luật mờ sinh ra có thể được các bác sĩ kiểm tra. Ví dụ, một tâm cụm có giá trị thalach thấp và oldpeak cao kèm theo kết luận "Nguy cơ cao" (xác suất ) là hoàn toàn phù hợp với tri thức y khoa về thiếu máu cơ tim.
Phần VI. Kết luận và hướng phát triển
Báo cáo cung cấp một cái nhìn toàn diện và sâu sắc về thuật toán Phân cụm Trừ và ứng dụng của nó trong y học.
- Về mặt lý thuyết: Phân cụm Trừ là lời giải thanh lịch cho bài toán xác định số lượng cụm, khắc phục được nhược điểm của K-Means và Mountain Clustering bằng cách sử dụng chính dữ liệu làm ứng viên tâm. Mối liên hệ toán học giữa và () là chìa khóa để chuyển đổi mượt mà từ miền hình học (cụm) sang miền logic (luật mờ).
- Về mặt thực tiễn: Việc áp dụng trên dữ liệu bệnh tim UCI cho thấy tính hiệu quả của phương pháp. Hệ thống không chỉ đưa ra chẩn đoán (Có/Không bệnh) mà còn cung cấp một cấu trúc luật minh bạch, giúp bác sĩ hiểu tại sao máy đưa ra quyết định đó (White-box AI).
Hướng phát triển: Để nâng cao độ chính xác lên mức >90% tiệm cận với các phương pháp Deep Learning, mô hình này nên được sử dụng làm bước khởi tạo (initialization) cho mạng ANFIS (Adaptive Neuro-Fuzzy Inference System). Sau khi có các luật thô từ Phân cụm Trừ, ta có thể dùng thuật toán Lan truyền ngược (Backpropagation) hoặc Lai ghép (Hybrid Learning) để tinh chỉnh các tham số tiền điều kiện () và hậu điều kiện () nhằm tối ưu hóa sai số trên tập dữ liệu huấn luyện.
Phụ lục
All Rights Reserved